ISO 3534-1:2006 Klausa 2.10 – 2.23 adalah Standar Internasional mengenai kosakata dan simbol statistik, khususnya tentang istilah statistik umum dan istilah yang digunakan dalam probabilitas.
Artikel ini merupakan lanjutan dari artikel sebelumnya berikut :
- ISO 3534-1 istilah probabilitas statistik
- ISO 3534-1:2006 Klausa 1.1 – 1.20
- ISO 3534-1:2006 Klausa 1.21 – 1.40
- ISO 3534-1 Klausa 1.41 – 1.65
- ISO 3534-1 Klausa 2.1-2.9
ISO 3534-1:2006 Klausa 2.10 – 2.23
ISO 3534-1:2006 Klausa 2.10
2.10 random variable : variabel acak
fungsi yang didefinisikan pada ruang sampel (2.1) di mana nilai-nilai fungsi diurutkan k-tuplet bilangan real
Contoh:
Melanjutkan contoh baterai yang diperkenalkan di 2.1, ruang sampel terdiri dari peristiwa yang dijelaskan dalam kata-kata (baterai gagal pada upaya awal, baterai bekerja pada awalnya tetapi kemudian gagal pada x jam).
Kejadian-kejadian seperti itu aneh untuk dikerjakan secara matematis, jadi wajar untuk mengaitkan dengan setiap kejadian, waktu (diberikan sebagai bilangan real) di mana baterai mati.
Jika variabel acak mengambil nilai 0, maka orang akan mengenali bahwa hasil ini sesuai dengan kegagalan awal.
Untuk nilai variabel acak yang lebih besar dari nol, dapat dipahami bahwa baterai pada awalnya bekerja dan kemudian gagal pada nilai spesifik ini.
Representasi variabel acak memungkinkan seseorang untuk menjawab pertanyaan seperti, “berapa probabilitas baterai melebihi masa garansi, yaitu 6 jam?”.
Catatan :
- 1 : Contoh k-tuplet terurut adalah (x1, x2, …, xk). Sebuah k-tuplet terurut adalah, dengan kata lain, sebuah vektor dalam k dimensi (baik vektor baris atau kolom).
- 2 : Biasanya, variabel acak memiliki dimensi yang dilambangkan dengan k. Jika k = 1, variabel acak dikatakan berdimensi satu atau univariat. Untuk k > 1, variabel acak dikatakan multidimensi.
Dalam praktiknya, ketika dimensi adalah bilangan tertentu, k, variabel acak dikatakan k-dimensi.
- 3 : Variabel acak satu dimensi adalah fungsi bernilai nyata yang didefinisikan pada ruang sampel (2.1) yang merupakan bagian dari ruang probabilitas (2.68).
- 4 : Variabel acak dengan nilai riil yang diberikan sebagai pasangan terurut dikatakan dua dimensi. Definisi tersebut memperluas konsep pasangan terurut ke k-tuplet terurut.
- 5 : Komponen ke-j dari variabel acak k-dimensi adalah variabel acak yang hanya sesuai dengan komponen ke-j dari k-tuplet. Komponen ke-j dari variabel acak k-dimensi sesuai dengan ruang probabilitas di mana peristiwa (2.2) ditentukan hanya dalam hal nilai komponen yang dipertimbangkan.
ISO 3534-1:2006 Klausa 2.11
2.11 probability distribution : distribusi peluang
distribution : distribusi
ukuran probabilitas (2,70) yang diinduksi oleh variabel acak (2,10)
Contoh:
- Melanjutkan contoh baterai dari 2.1, distribusi masa pakai baterai sepenuhnya menggambarkan probabilitas terjadinya nilai-nilai tertentu. Tidak diketahui dengan pasti berapa lama waktu kegagalan baterai yang diberikan juga tidak diketahui (sebelum pengujian) apakah baterai akan berfungsi pada upaya awal. Distribusi probabilitas sepenuhnya menggambarkan sifat probabilistik dari hasil yang tidak pasti. Dalam Catatan 4 dari 2.7, satu kemungkinan representasi dari distribusi probabilitas diberikan, yaitu fungsi distribusi.
Catatan :
- 1 : Ada banyak, representasi matematis yang setara dari suatu distribusi termasuk fungsi distribusi (2.7), fungsi kepadatan probabilitas (2.27), jika ada, dan fungsi karakteristik. Dengan berbagai tingkat kesulitan, representasi ini memungkinkan untuk menentukan probabilitas dengan mana variabel acak mengambil nilai di wilayah tertentu.
- 2 : Karena variabel acak adalah fungsi pada himpunan bagian dari ruang sampel ke garis nyata, maka kasusnya, misalnya, probabilitas bahwa variabel acak mengambil nilai riil apa pun adalah 1.
Untuk contoh baterai , P[X 0] = 1. Dalam banyak situasi, jauh lebih mudah untuk berurusan langsung dengan variabel acak dan salah satu representasinya daripada memperhatikan ukuran probabilitas yang mendasarinya.
Namun, dalam mengonversi dari satu representasi ke representasi lainnya, ukuran probabilitas memastikan konsistensi.
- 3 : Variabel acak dengan komponen tunggal disebut distribusi probabilitas satu dimensi atau univariat.
Jika variabel acak memiliki dua komponen, satu berbicara tentang distribusi probabilitas dua dimensi atau bivariat, dan dengan lebih dari dua komponen, variabel acak memiliki distribusi probabilitas multidimensi atau multivariat.
ISO 3534-1:2006 Klausa 2.12
2.12 expectation : ekspektasi
integral dari fungsi variabel acak (2,10) sehubungan dengan ukuran probabilitas (2,70) di atas ruang sampel (2,1)
Catatan :
- 1 : Ekspektasi fungsi g dari variabel acakX dilambangkan dengan E[g(X)] dan dihitung sebagai:
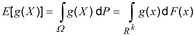
di mana F(x) adalah fungsi distribusi yang sesuai.
- 2 : “E” dalam E[g(X)] berasal dari “nilai yang diharapkan” atau “harapan” dari variabel acak X. E dapat dilihat sebagai operator atau fungsi yang memetakan variabel acak ke garis nyata menurut perhitungan di atas.
- 3 : Dua integral diberikan untuk E[g(X)]. Yang pertama memperlakukan integrasi atas ruang sampel yang secara konseptual menarik tetapi tidak praktis, karena alasan kecanggungan dalam menangani peristiwa itu sendiri (misalnya, jika diberikan secara verbal). Integral kedua menggambarkan perhitungan atas Rk, yang merupakan kepentingan praktis yang lebih besar.
- 4 : Dalam banyak kasus kepentingan praktis, integral di atas direduksi menjadi bentuk yang dapat dikenali dari kalkulus. Contoh diberikan dalam catatan untuk momen orde (2,34) di mana g(x) = xr, mean (2,35) di mana g(x) = x dan varians (2,36) di mana g(x) = [x E(X) ]2.
- 5 : Definisi ini tidak terbatas pada integral satu dimensi seperti yang mungkin disarankan oleh contoh dan catatan sebelumnya. Untuk situasi dimensi yang lebih tinggi, lihat 2.43.
- 6 : Untuk variabel acak diskrit (2,28), integral kedua dalam Catatan 1 diganti dengan simbol penjumlahan. Contohnya dapat ditemukan di 2.35.
ISO 3534-1:2006 Klausa 2.13
2.13 p-quantile : p-kuantil
p-fractile : p-fraktil
Xp,xp : Xp,xp
nilai x sama dengan infimum semua x sedemikian rupa sehingga fungsi distribusi (2.7)F(x) lebih besar dari atau sama dengan p, untuk 0 < p < 1
Contoh 1:
Pertimbangkan distribusi binomial (2,46) dengan fungsi massa probabilitas yang diberikan pada Tabel 2. Kumpulan nilai ini sesuai dengan distribusi binomial dengan parameter n = 6 dan p = 0,3. Untuk kasus ini, beberapa kuantil p yang dipilih adalah:
- x0,1 = 0
- x0,25 = 1
- x0,5 = 2
- x0,75 = 3
- x0,90 = 3
- x0,95 = 4
- x0,99 = 5
- x0,999 = 5
Diskrit dari distribusi binomial mengarah ke nilai integral dari p-kuantil.
Tabel 2 — Contoh distribusi binomial
| X | P[X = x] | P[X ≤ x] | P[X > x] |
| 0 | 0,117 649 | 0,117 649 | 0,882 351 |
| 1 | 0,302 526 | 0,420 175 | 0,579 825 |
| 2 | 0,324 135 | 0,744 310 | 0,255 690 |
| 3 | 0,185 220 | 0,929 530 | 0,070 470 |
| 4 | 0,059 535 | 0,989 065 | 0,010 935 |
| 5 | 0,010 206 | 0,999 271 | 0,000 729 |
| 6 | 0,000 729 | 1,000 000 | 0,000 000 |
Contoh 2:
Pertimbangkan distribusi normal standar (2.51) dengan nilai yang dipilih dari fungsi distribusi yang diberikan pada Tabel 3. Beberapa p-kuantil yang dipilih adalah:
Tabel 3 — Contoh distribusi normal terstandardisasi
| p | x such that P[X ≤ x] = p |
| 0,1 | −1,282 |
| 0,25 | −0,674 |
| 0,5 | 0,000 |
| 0,75 | 0,674 |
| 0,841 344 75 | 1,000 |
| 0,9 | 1,282 |
| 0,95 | 1,645 |
| 0,975 | 1,960 |
| 0,99 | 2,326 |
| 0,995 | 2,576 |
| 0,999 | 3,090 |
Karena distribusi X kontinu, judul kolom kedua juga dapat berupa: x sehingga P[X > x] = p.
Catatan :
- 1 : Untuk distribusi kontinu (2,23), jika p adalah 0,5 maka kuantil 0,5 sesuai dengan median (2,14). Untuk p sama dengan 0,25, kuantil 0,25 dikenal sebagai kuartil bawah. Untuk distribusi kontinu, 25% distribusi berada di bawah kuantil 0,25 sedangkan 75% berada di atas kuantil 0,25. Untuk p sama dengan 0,75, kuartil 0,75 dikenal sebagai kuartil atas.
- 2 : Secara umum, 100 p % dari suatu distribusi berada di bawah p-kuantil; 100(1 p) % dari suatu distribusi berada di atas p-kuantil. Ada kesulitan dalam mendefinisikan median untuk distribusi diskrit karena dapat dikatakan memiliki beberapa nilai yang memenuhi definisi.
- 3 : Jika F kontinu dan benar-benar meningkat, kuantil p adalah solusi untuk F(x) = p. Dalam hal ini, kata “infimum” dalam definisi tersebut dapat diganti dengan “minimum”.
- 4 : Jika fungsi distribusi konstan dan sama dengan p dalam suatu interval, maka semua nilai dalam interval tersebut adalah p-kuantil untuk F.
- 5 : p-kuantil didefinisikan untuk distribusi univariat (2.16).
Klausa 2.14 – 2.16
2.14 median
0,5-kuantil (2.13)
Contoh:
- Untuk contoh baterai Note 4 di 2.7, median adalah 0,587 8, yang merupakan solusi untuk x dalam 0,1 + 0,9[1−exp(−x)] = 0,5
Catatan :
- 1 : Median adalah salah satu kuantil p (2.13) yang paling umum diterapkan dalam penggunaan praktis. Median distribusi univariat kontinu (2.16) adalah sedemikian rupa sehingga setengah dari populasi (1,1) lebih besar dari atau sama dengan median dan setengah dari populasi kurang dari atau sama dengan median.
- 2 : Median didefinisikan untuk distribusi univariat (2.16).
2.15 quartile : kuartil
0,25-kuantil (2.13) atau 0,75-kuantil
Contoh:
- Melanjutkan contoh baterai 2.14, dapat ditunjukkan bahwa kuantil 0,25 adalah 0,182 3 dan kuantil 0,75 adalah 1,280 9.
Catatan :
- 1 : Kuartil 0,25 juga dikenal sebagai kuartil bawah, sedangkan kuartil 0,75 juga dikenal sebagai kuartil atas.
- 2 : Kuartil didefinisikan untuk distribusi univariat (2.16).
2.16 univariate probability distribution : distribusi probabilitas univariat
univariate distribution : distribusi univariat
distribusi probabilitas (2.11) dari variabel acak tunggal (2.10)
- Catatan 1 : Distribusi probabilitas univariat adalah satu dimensi. Distribusi binomial (2,46), Poisson (2,47), normal (2,50), gamma (2,56), t (2,53), Weibull (2,63) dan beta (2,59) adalah contoh distribusi probabilitas univariat.
Klausa 2.17
2.17 multivariate probability distribution : distribusi probabilitas multivariat
multivariate distribution : distribusi multivariat
distribusi probabilitas (2.11) dari dua atau lebih variabel acak (2.10)
Catatan :
- 1 : Untuk distribusi probabilitas dengan tepat dua variabel acak, multivariat kualifikasi sering diganti dengan bivariat kualifikasi yang lebih restriktif. Seperti disebutkan dalam Kata Pengantar, distribusi probabilitas dari variabel acak tunggal dapat secara eksplisit disebut distribusi satu dimensi atau univariat (2.16). Karena situasi ini lebih dominan, biasanya menganggap situasi univariat kecuali dinyatakan lain.
- 2 : Distribusi multivariat kadang-kadang disebut sebagai distribusi bersama.
- 3 : Distribusi multinomial (2,45), distribusi normal bivariat (2,65) dan distribusi normal multivariat (2,64) adalah contoh distribusi probabilitas multivariat yang tercakup dalam bagian ISO 3534 ini.
Klausa 2.18
2.18 marginal probability distribution : distribusi probabilitas marjinal
marginal distribution : distribusi marjinal
distribusi probabilitas (2.11) dari subset ketat yang tidak kosong dari komponen variabel acak (2.10)
Contoh :
- 1: Untuk distribusi dengan tiga variabel acak X, Y dan Z, terdapat tiga distribusi marginal dengan dua variabel acak, yaitu untuk (X, Y), (X, Z) dan (Y, Z) dan tiga distribusi marginal dengan satu variabel, yaitu untuk X, Y dan Z.
- 2: Untuk distribusi normal bivariat (2,65) dari pasangan variabel (X,Y), distribusi masing-masing variabel X dan Y yang dianggap terpisah adalah distribusi marginal, yang keduanya merupakan distribusi normal (2,50).
- 3: Untuk distribusi multinomial (2,45), distribusi (X1, X2) adalah distribusi marginal jika k > 3. Distribusi X1, X2, …, Xk, secara terpisah juga merupakan distribusi marginal. Distribusi marginal ini masing-masing merupakan distribusi binomial (2,46).
Catatan :
- 1 : Untuk distribusi gabungan dalam k dimensi, salah satu contoh distribusi marjinal mencakup distribusi probabilitas dari subset k1 < k variabel acak.
- 2 : Diberikan distribusi probabilitas multivariat kontinu (2.23) (2.17) yang diwakili oleh fungsi kepadatan probabilitasnya (2.26), fungsi kepadatan probabilitas dari distribusi probabilitas marjinalnya ditentukan dengan mengintegrasikan fungsi kepadatan probabilitas di atas domain variabel yang tidak diperhitungkan dalam distribusi marginal.
- 3 : Diberikan distribusi probabilitas multivariat diskrit (2.22) yang diwakili oleh fungsi massa probabilitasnya (2.24), fungsi massa probabilitas dari distribusi probabilitas marjinalnya ditentukan dengan menjumlahkan fungsi massa probabilitas atas domain variabel yang tidak dipertimbangkan dalam distribusi marjinal.
Klausa 2.19
2.19 conditional probability distribution : distribusi probabilitas bersyarat
conditional distribution : distribusi bersyarat
distribusi probabilitas (2.11) terbatas pada subset tidak kosong dari ruang sampel (2.1) dan disesuaikan untuk memiliki probabilitas total satu pada ruang sampel terbatas
Contoh :
- 1: Dalam contoh baterai 2.7, Catatan 4, distribusi kondisional masa pakai baterai mengingat fungsi baterai pada awalnya adalah eksponensial (2.58).
- 2: Untuk distribusi normal bivariat (2,65), distribusi probabilitas bersyarat dari Y mengingat bahwa X = x mencerminkan dampak pada Y dari pengetahuan tentang X.
- 3: Pertimbangkan variabel acak X yang menggambarkan distribusi biaya kerugian tahunan yang diasuransikan di Florida karena peristiwa badai yang diumumkan. Distribusi ini akan memiliki probabilitas nol nol biaya kerugian tahunan karena kemungkinan bahwa tidak ada badai yang berdampak pada Florida pada tahun tertentu. Yang mungkin menarik adalah distribusi bersyarat dari biaya kerugian untuk tahun-tahun di mana suatu peristiwa benar-benar terjadi.
Catatan :
- 1 : Sebagai contoh untuk distribusi dengan dua variabel acak X dan Y, ada distribusi bersyarat untuk X dan distribusi bersyarat untuk Y. Distribusi X yang dikondisikan melalui Y = y dilambangkan sebagai “distribusi bersyarat dari X diberikan Y = y”, sedangkan distribusi Y yang dikondisikan oleh X = x dilambangkan dengan “distribusi bersyarat dari Y yang diberikan X = x”.
- 2 : Distribusi probabilitas marjinal (2.18) dapat dilihat sebagai distribusi tak bersyarat.
- 3 : Contoh 1 di atas menggambarkan situasi di mana distribusi univariat disesuaikan melalui pengkondisian untuk menghasilkan distribusi univariat lain, yang dalam hal ini adalah distribusi yang berbeda. Sebaliknya, untuk distribusi eksponensial, distribusi bersyarat bahwa kegagalan akan terjadi dalam satu jam berikutnya, mengingat tidak ada kegagalan yang terjadi selama 10 jam pertama, adalah eksponensial dengan parameter yang sama.
- 4 : Distribusi bersyarat dapat muncul untuk distribusi diskrit tertentu di mana hasil spesifik tidak mungkin. Misalnya, distribusi Poisson dapat berfungsi sebagai model untuk jumlah pasien kanker dalam populasi pasien yang terinfeksi jika dikondisikan untuk benar-benar positif (pasien tanpa tumor menurut definisinya tidak terinfeksi).
- 5 : Distribusi bersyarat muncul dalam konteks membatasi ruang sampel ke subset tertentu. Untuk (X, Y) yang memiliki distribusi normal bivariat (2,65) mungkin menarik untuk mempertimbangkan distribusi bersyarat dari (X, Y) mengingat bahwa hasilnya harus terjadi pada kuadrat satuan [0, 1] × [0, 1 ]. Kemungkinan lain adalah distribusi bersyarat (X, Y) mengingat X2 + Y2 r. Kasus ini sesuai dengan situasi di mana misalnya bagian memenuhi toleransi dan orang mungkin tertarik pada properti lebih lanjut berdasarkan pencapaian kinerja ini.
Klausa 2.20 – 2.22
2.20 regression curve : kurva regresi
kumpulan nilai-nilai harapan (2,12) dari distribusi probabilitas bersyarat (2,19) dari variabel acak (2,10) Y diberikan variabel acak X = x
- Catatan 1 : Di sini, kurva regresi didefinisikan dalam konteks (X, Y) yang memiliki distribusi bivariat (lihat Catatan 1 hingga 2.17). Oleh karena itu, ini adalah konsep yang berbeda dari yang ditemukan dalam analisis regresi di mana Y terkait dengan seperangkat nilai independen deterministik.
2.21 regression surface : permukaan regresi
kumpulan nilai-nilai harapan (2,12) dari distribusi probabilitas bersyarat (2,19) dari variabel acak (2,10) Y dengan variabel acak X1 = x1 dan X2 = x2
- Catatan 1 : Di sini, seperti pada 2.20, permukaan regresi didefinisikan dalam konteks (Y, X1, X2 ) sebagai distribusi multivariat (2,17). Seperti kurva regresi, permukaan regresi melibatkan konsep yang berbeda dari yang ditemukan dalam analisis regresi dan metodologi permukaan respons.
2.22 discrete probability distribution : distribusi probabilitas diskrit
discrete distribution : distribusi diskrit
distribusi probabilitas (2.11) di mana ruang sampelΩ (2.1) terbatas atau tak terbatas
Contoh:
- Contoh distribusi diskrit dalam dokumen ini adalah multinomial (2,45), binomial (2,46), Poisson (2,47), hipergeometrik (2,48), dan binomial negatif (2,49).
Catatan :
- 1 : “Diskrit” menyiratkan bahwa ruang sampel dapat diberikan dalam daftar hingga atau awal dari daftar tak terbatas di mana pola berikutnya terlihat, seperti jumlah cacat menjadi 0, 1, 2, … Selain itu , distribusi binomial sesuai dengan ruang sampel berhingga {0, 1, 2, …, n} sedangkan distribusi Poisson sesuai dengan ruang sampel tak hingga {0, 1, 2, …}.
- 2 : Situasi dengan data atribut dalam pengambilan sampel penerimaan melibatkan distribusi diskrit.
- 3 : Fungsi distribusi (2.7) dari distribusi diskrit dinilai diskrit.
Klausa 2.23
2.23 continuous probability distribution : distribusi probabilitas kontinu
continuous distribution : distribusi berkelanjutan
distribusi probabilitas (2.11) dimana fungsi distribusi (2.7) dievaluasi pada x dapat dinyatakan sebagai integral dari fungsi non-negatif dari ke x
CONTOH:
Situasi di mana distribusi kontinu terjadi hampir semua yang melibatkan tipe data variabel yang ditemukan dalam aplikasi industri.
Catatan :
- 1 : Contoh distribusi kontinu adalah normal (2,50), normal standar (2,51), t (2,53), F (2,55), gamma (2,56), chi-kuadrat (2,57), eksponensial (2,58), beta ( 2,59), seragam (2,60), nilai ekstrim Tipe I (2,61), nilai ekstrim Tipe II (2,62), nilai ekstrim Tipe III (2,63), dan lognormal (2,52).
- 2 : Fungsi non-negatif yang dirujuk dalam definisi adalah fungsi kepadatan probabilitas (2,26). Hal ini terlalu membatasi untuk bersikeras bahwa fungsi distribusi dapat dibedakan di mana-mana.
Namun, untuk pertimbangan praktis, banyak distribusi kontinu yang umum digunakan memiliki sifat bahwa turunan dari fungsi distribusi menyediakan fungsi kerapatan probabilitas yang sesuai.
- 3 : Situasi dengan data variabel dalam aplikasi pengambilan sampel penerimaan sesuai dengan distribusi probabilitas berkelanjutan
ISO 3534-1:2006 Klausa 2.24
Dikarenakan isi Klausa 1 dan 2 ini terlalu panjang, maka pembaca bisa melanjutkan ke artikel lanjutan dari standarku.com berikut :
- ISO 3534-1 Klausa 2.24 – 2.48
- ISO 3534-1 Klausa 2.49 – 2.70
Penutup
Demikian artikel dari standarku.com mengenai Standar ISO 3534-1:2006.
Mohon saran dari pembaca untuk kelengkapan isi artikel ini, silahkan saran tersebut dapat disampaikan melalui kolom komentar.
Baca artikel lain :
- International Organization for Standardization
- Memahami apa itu Standar ISO
- Memahami Standard atau Standar
Sumber referensi :