ISO 3534-1:2006 Klausa 1.21 – 1.40 adalah Standar Internasional mengenai kosakata dan simbol statistik, khususnya tentang istilah statistik umum dan istilah yang digunakan dalam probabilitas.
Artikel ini merupakan lanjutan dari artikel sebelumnya berikut :
ISO 3534-1:2006 Klausa 1.21 – 1.40
Klausa 1.21
1.21 sample coefficient of kurtosis : koefisien sampel kurtosis
rata-rata aritmatika pangkat keempat dari variabel acak sampel standar (1,19) dari sampel acak (1,6)
CONTOH:
Melanjutkan contoh dari 1,9, koefisien sampel kurtosis yang diamati dapat dihitung menjadi 2,674 19.
Untuk ukuran sampel seperti 10 dalam contoh ini, koefisien sampel kurtosis sangat bervariasi, sehingga harus digunakan dengan hati-hati.
Paket statistik menggunakan berbagai penyesuaian dalam menghitung koefisien sampel kurtosis (lihat Catatan 3 dari 2.40).
Menggunakan rumus alternatif yang diberikan dalam Catatan 1, nilai yang dihitung adalah 0,436 05.
Kedua nilai 2,674 19 dan 0,436 05 tidak dapat dibandingkan secara langsung.
Untuk melakukannya, ambil 2,674 19 – 3 (untuk menghubungkan kurtosis dari distribusi normal yaitu 3) yang sama dengan 0,325 81 yang sekarang dapat dibandingkan dengan 0,436 05.
Catatan :
- 1 : Rumus yang sesuai dengan definisi adalah:

Beberapa paket statistik menggunakan rumus berikut untuk koefisien sampel kurtosis untuk mengoreksi bias (1,33) dan untuk menunjukkan penyimpangan dari kurtosis dari distribusi normal (yang sama dengan 3):
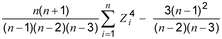
di mana
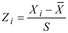
Suku kedua dalam ekspresi adalah sekitar 3 untuk n besar. Terkadang kurtosis dilaporkan sebagai nilai seperti yang didefinisikan dalam 2,40 dikurangi 3 untuk menekankan perbandingan dengan distribusi normal.
Jelas, seorang praktisi perlu menyadari penyesuaian, jika ada, dalam perhitungan paket statistik.
- 2 : Kurtosis mengacu pada beratnya ekor distribusi (unimodal). Untuk distribusi normal (2,50), koefisien sampel kurtosis kira-kira 3, tergantung pada variabilitas sampling. Dalam prakteknya, kurtosis dari distribusi normal memberikan patokan atau nilai dasar. Distribusi (2.11) dengan nilai lebih kecil dari 3 memiliki ekor yang lebih ringan dari distribusi normal; distribusi dengan nilai lebih besar dari 3 memiliki ekor yang lebih berat dari distribusi normal.
- 3 : Untuk nilai kurtosis yang diamati jauh lebih besar dari 3, ada kemungkinan bahwa distribusi yang mendasarinya memiliki ekor yang benar-benar lebih berat daripada distribusi normal. Sampel dapat terkontaminasi oleh pengamatan dari sumber lain atau dari kesalahan pengkodean.
- 4 : Koefisien sampel kurtosis dapat dikenali sebagai momen sampel ke-4 dari variabel acak sampel standar.
Klausa 1.22
1.22 sample covariance ( SXY)
jumlah produk simpangan pasangan variabel acak (2,10) dalam sampel acak (1,6) dari rata-rata sampelnya (1,15) dibagi dengan jumlah suku dalam jumlah dikurangi satu
CONTOH 1:
Perhatikan ilustrasi numerik berikut dengan menggunakan 10 nilai 3-tupel (kembar tiga) yang diamati. Untuk contoh ini, pertimbangkan hanya x dan y.
Tabel 1 — Hasil untuk Contoh 1
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x | 38 | 41 | 24 | 60 | 41 | 51 | 58 | 50 | 65 | 33 |
| y | 73 | 74 | 43 | 107 | 65 | 73 | 99 | 72 | 100 | 48 |
| z | 34 | 31 | 40 | 28 | 35 | 28 | 32 | 27 | 27 | 31 |
Rata-rata sampel yang diamati untuk X adalah 46,1 dan untuk Y adalah 75,4. Kovarians sampel sama dengan
[(38 46,1) × (73 75,4) + (41 46,1) × (74 75,4) + … + (33 46,1) × (48 75,4) ]/9 = 257.178
CONTOH 2:
Dalam tabel contoh sebelumnya, pertimbangkan hanya y dan z. Rata-rata sampel yang diamati untuk Z adalah 31,3. Kovarians sampel sama dengan
[(73 75,4) × (34 31,3) + (74 75,4) × (74 31,3) + … + (48 75,4) × (31 31,3) ]/9 = 54.356
Catatan :
- 1 : Dianggap sebagai statistik (1.8) kovarians sampel adalah fungsi dari pasangan variabel acak [(X1, Y1 ), (X2, Y2 ), …, (Xn, Yn)] dari sampel acak ukuran n dalam arti yang diberikan dalam Catatan 3 dari 1.6. Penduga ini (1.12) perlu dibedakan dari nilai numerik kovarians sampel yang dihitung dari pasangan nilai unit sampling yang diamati (1.2) [(x1, y1), (x2, y2), …, (xn , yn)] dalam sampel acak. Nilai numerik ini disebut kovarians sampel empiris atau kovarians sampel yang diamati.
- 2 : Sampel kovarians SXY diberikan sebagai:
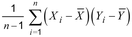
- 3 : Menggunakan n 1 memberikan penduga tak bias (1,34) dari kovarians populasi (2,43).
- 4 : Contoh pada Tabel 1 terdiri dari tiga variabel sedangkan definisi mengacu pada sepasang variabel. Dalam praktiknya, adalah umum untuk menghadapi situasi dengan banyak variabel.
Klausa 1.23
1.23 sample correlation coefficient (rxy) : koefisien korelasi sampel
kovarians sampel (1,22) dibagi dengan produk dari standar deviasi sampel yang sesuai (1,17)
CONTOH 1:
Melanjutkan Contoh 1 dari 1.22, deviasi standar yang diamati adalah 12.948 untuk X dan 21.329 untuk Y. Oleh karena itu, koefisien korelasi sampel yang diamati (untuk X dan Y) diberikan oleh:
257.178/(12.948 × 21.329) = 0,931 2
CONTOH 2:
Melanjutkan Contoh 2 dari 1.22, standar deviasi yang diamati adalah 21.329 untuk Y dan 4.165 untuk Z. Oleh karena itu, koefisien korelasi sampel yang diamati (untuk Y dan Z) diberikan oleh:
54.356/(21.329 × 4.165) = 0.612
Catatan :
- 1 : Secara notasi, koefisien korelasi sampel dihitung sebagai:
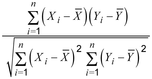
Ekspresi ini setara dengan rasio kovarians sampel dengan akar kuadrat dari produk varians sampel. Terkadang simbol rxy digunakan untuk menunjukkan koefisien korelasi sampel. Koefisien korelasi sampel yang diamati didasarkan pada realisasi (x1, y1), (x2, y2), …, (xn, yn).
- 2 : Koefisien korelasi sampel yang diamati dapat mengambil nilai dalam [−1, 1], dengan nilai yang mendekati 1 menunjukkan korelasi positif yang kuat dan nilai yang mendekati -1 menunjukkan korelasi negatif yang kuat. Koefisien korelasi sampel menunjukkan derajat hubungan linier antara dua variabel, dengan nilai mendekati -1 atau 1 menunjukkan hubungan linier yang kuat sedangkan nilai yang mendekati 0 menunjukkan hubungan linier yang lemah.
Klausa 1.24 – 1.26
1.24 standard error : kesalahan standar
simpangan baku (2,37) dari penaksir (1.12)
CONTOH:
- Jika mean sampel (1,15) adalah penaksir mean populasi (2,35) dan simpangan baku variabel acak tunggal (2,10) adalah , maka galat standar mean sampel adalah di mana n adalah jumlah pengamatan dalam Sampel. Penduga kesalahan standar adalah di mana S adalah standar deviasi sampel (1,17).
Catatan :
- 1 : Dalam praktiknya, kesalahan standar memberikan perkiraan alami dari standar deviasi penduga.
- 2 : Tidak ada kesalahan istilah pelengkap (yang masuk akal) “non-standar”. Kesalahan standar dapat dilihat sebagai singkatan untuk ekspresi “standar deviasi penaksir”. Umumnya, dalam praktiknya, kesalahan standar secara implisit mengacu pada standar deviasi rata-rata sampel. Notasi untuk kesalahan standar rata-rata sampel adalah .
1.25 interval estimator : penaksir interval
interval, dibatasi oleh statistik batas atas (1,8) dan statistik batas bawah
Catatan :
- 1 : Salah satu titik akhir dapat berupa +∞, atau batas alami dari nilai parameter. Misalnya, 0 adalah batas bawah alami untuk penduga interval varians populasi (2,36). Dalam kasus seperti itu, interval biasanya disebut sebagai interval satu sisi.
- 2 : Penaksir interval dapat diberikan bersama dengan estimasi parameter (2.9) (1.36). Penaksir interval dianggap mengandung parameter pada proporsi kejadian tertentu, dalam kondisi pengambilan sampel berulang, atau dalam beberapa pengertian probabilistik lainnya.
- 3 : Tiga jenis penduga interval yang umum mencakup interval kepercayaan (1,28) untuk parameter, interval prediksi (1,30) untuk pengamatan masa depan, dan interval toleransi statistik (1,26) pada proporsi distribusi (2,11) yang terkandung.
1.26 statistical tolerance interval : interval toleransi statistik
interval ditentukan dari sampel acak (1.6) sedemikian rupa sehingga seseorang dapat memiliki tingkat kepercayaan tertentu bahwa interval tersebut mencakup setidaknya proporsi tertentu dari populasi sampel (1.1)
- Catatan 1 : Keyakinan dalam konteks ini adalah proporsi jangka panjang dari interval yang dibangun dengan cara ini yang akan mencakup setidaknya proporsi tertentu dari populasi sampel.
Klausa 1.27 – 1.28
1.27 statistical tolerance limit : batas toleransi statistik
statistik (1,8) mewakili titik akhir dari interval toleransi statistik (1,26)
Catatan 1 : Interval toleransi statistik dapat berupa :
- — satu sisi (dengan salah satu batasnya ditetapkan pada batas alami variabel acak), dalam hal ini mereka memiliki batas toleransi statistik atas atau bawah, atau
- — dua sisi, dalam hal ini keduanya memiliki keduanya. Batas alami dari variabel acak dapat memberikan batas untuk batas satu sisi.
1.28 confidence interval : selang kepercayaan
penduga interval (1,25) (T0, T1 ) untuk parameter (2.9)θ dengan statistik (1.8)T0 dan T1 sebagai batas interval dan yang menyatakan bahwa P [ T0 < θ < T1 ] ≥ 1
Catatan :
- 1 : Keyakinan mencerminkan proporsi kasus bahwa interval kepercayaan akan berisi nilai parameter sebenarnya dalam serangkaian panjang sampel acak berulang (1,6) di bawah kondisi yang identik. Interval kepercayaan tidak mencerminkan probabilitas (2,5) bahwa interval yang diamati berisi nilai sebenarnya dari parameter (ia mengandung atau tidak mengandungnya).
- 2 : Terkait dengan interval kepercayaan ini adalah karakteristik kinerja petugas 100(1 ) %, di mana umumnya merupakan angka kecil. Karakteristik kinerja, yang disebut koefisien kepercayaan atau tingkat kepercayaan, seringkali 95% atau 99%. Pertidaksamaan P [T0 < < T1 ] 1 berlaku untuk nilai populasi yang spesifik tetapi tidak diketahui.
Klausa 1.29 – 1.30
1.29 one-sided confidence interval : interval kepercayaan satu sisi
interval kepercayaan (1,28) dengan salah satu titik ujungnya tetap pada +∞, , atau batas tetap alami
Catatan :
- 1 : Definisi 1.28 berlaku baik dengan T0 ditetapkan pada atau T1 ditetapkan pada +∞. Interval kepercayaan satu sisi muncul dalam situasi di mana minat hanya terfokus pada satu arah. Misalnya, dalam pengujian volume audio untuk masalah keamanan di telepon seluler, batas kepercayaan atas akan menarik yang menunjukkan batas atas untuk volume yang dihasilkan dalam kondisi yang dianggap aman. Untuk pengujian mekanis struktural, batas kepercayaan yang lebih rendah pada gaya di mana perangkat gagal akan menarik.
- 2 : Contoh lain dari interval kepercayaan satu sisi terjadi dalam situasi di mana parameter memiliki batas alami seperti nol. Untuk distribusi Poisson (2.47) yang terlibat dalam pemodelan keluhan pelanggan, nol adalah batas bawah. Sebagai contoh lain, interval kepercayaan untuk keandalan komponen elektronik dapat menjadi (0,98, 1), di mana 1 adalah batas batas atas alami.
1.30 prediction interval : interval prediksi
rentang nilai suatu variabel, yang diturunkan dari sampel acak (1,6) nilai dari populasi kontinu, di mana variabel tersebut dapat ditegaskan dengan keyakinan tertentu bahwa tidak kurang dari sejumlah nilai tertentu dalam sampel acak lebih lanjut dari populasi yang sama (1.1) akan jatuh
- Catatan 1 : Umumnya, minat berfokus pada satu pengamatan lebih lanjut yang timbul dari situasi yang sama dengan pengamatan yang menjadi dasar interval prediksi. Konteks praktis lainnya adalah analisis regresi di mana interval prediksi dibangun untuk spektrum nilai independen.
Klausa 1.31 – 1.33
1.31 estimate : memperkirakan
nilai yang diamati (1.4) dari estimator (1.12)
- Catatan 1 : Estimasi mengacu pada nilai numerik yang diperoleh dari nilai yang diamati. Sehubungan dengan estimasi (1,36) parameter (2,9) dari distribusi probabilitas yang dihipotesiskan (2,11), estimator mengacu pada statistik (1,8) yang dimaksudkan untuk memperkirakan parameter dan estimasi mengacu pada hasil menggunakan nilai yang diamati. Kadang-kadang kata sifat “titik” disisipkan sebelum perkiraan untuk menekankan bahwa satu nilai sedang diproduksi daripada interval nilai. Demikian pula, kata sifat “interval” dimasukkan sebelum estimasi dalam kasus di mana estimasi interval berlangsung.
1.32 error of estimation : kesalahan estimasi
estimasi (1.31) dikurangi parameter (2.9) atau properti populasi yang dimaksudkan untuk diestimasi
Catatan :
- 1 : Properti populasi mungkin merupakan fungsi dari parameter atau parameter atau kuantitas lain yang terkait dengan distribusi probabilitas (2.11).
- 2 : Kesalahan penaksir dapat melibatkan kontribusi karena pengambilan sampel, ketidakpastian pengukuran, pembulatan, atau sumber lainnya. Akibatnya, kesalahan estimator mewakili kinerja garis bawah yang menarik bagi para praktisi. Menentukan kontributor utama kesalahan estimator adalah elemen penting dalam upaya peningkatan kualitas.
1.33 bias : bias
ekspektasi (2.12) dari kesalahan estimasi (1.32)
Catatan :
- 1 : Definisi ini berbeda dari ISO 3534-2:2006 (3.3.2) dan VIM:1993 (5.25 dan 5.28). Di sini bias digunakan dalam pengertian umum seperti yang ditunjukkan dalam Catatan 1 di 1.34.
- 2 : Adanya bias dapat menyebabkan konsekuensi yang tidak menguntungkan dalam praktik. Misalnya, meremehkan kekuatan material karena bias dapat menyebabkan kegagalan perangkat yang tidak terduga. Dalam pengambilan sampel survei, bias dapat menyebabkan keputusan yang salah dari jajak pendapat politik.
Klausa 1.34
1.34 unbiased estimator : penaksir tak bias
estimator (1.12) memiliki bias (1.33) sama dengan nol
Contoh :
- 1: Untuk sampel acak (1,6) dari n variabel acak independen (2,10), masing-masing dengan distribusi normal yang sama (2,50) dengan mean (2,35) dan standar deviasi (2,37)σ, mean sampel (1,15) dan varians sampel ( 1.16)S2 adalah estimator tak bias untuk rata-rata dan varians (2.36)σ2, masing-masing.
- 2: Seperti disebutkan dalam Catatan 1 hingga 1,37 penduga kemungkinan maksimum (1,35) dari varians 2 menggunakan penyebut n alih-alih n 1 dan dengan demikian merupakan penaksir bias. Dalam aplikasi, deviasi standar sampel (1,17) menerima banyak penggunaan tetapi penting untuk dicatat bahwa akar kuadrat dari varians sampel menggunakan n 1 adalah penaksir bias dari deviasi standar populasi (2,37).
- 3: Untuk sampel acak dari n pasangan variabel acak independen, setiap pasangan dengan distribusi normal bivariat yang sama (2,65) dengan kovarians (2,43) sama dengan XY, kovarians sampel (1,22) adalah penduga tak bias untuk kovarians populasi. Penaksir kemungkinan maksimum menggunakan n alih-alih n 1 dalam penyebut dan dengan demikian menjadi bias.
Catatan 1 :
- Penaksir yang tidak bias diinginkan karena rata-rata, mereka memberikan nilai yang benar. Tentu saja, penduga tak bias memberikan titik awal yang berguna dalam pencarian penduga parameter populasi yang “optimal”. Definisi yang diberikan di sini bersifat statistik. Dalam penggunaan sehari-hari, praktisi mencoba menghindari bias ke dalam penelitian dengan memastikan, misalnya, bahwa sampel acak mewakili populasi yang diinginkan.
Klausa 1.35 – 1.36
1.35 maximum likelihood estimator : penaksir kemungkinan maksimum
estimator (1.12) menetapkan nilai parameter (2.9) di mana fungsi kemungkinan (1.38) mencapai atau mendekati nilai tertingginya
Catatan :
- 1 : Estimasi kemungkinan maksimum adalah pendekatan yang mapan untuk memperoleh estimasi parameter di mana distribusi (2.11) telah ditentukan [misalnya, normal (2,50), gamma (2,56), Weibull (2,63), dan seterusnya] . Penduga ini memiliki sifat statistik yang diinginkan (misalnya, invarian di bawah transformasi monoton) dan dalam banyak situasi menyediakan metode estimasi pilihan. Dalam kasus di mana penduga kemungkinan maksimum bias, koreksi bias sederhana (1.33) kadang-kadang terjadi. Seperti disebutkan dalam Contoh 2 dari 1,34 penduga kemungkinan maksimum untuk varians (2,36) dari distribusi normal bias tetapi dapat dikoreksi dengan menggunakan n 1 daripada n. Tingkat bias dalam kasus tersebut menurun dengan meningkatnya ukuran sampel.
- 2 : Singkatan MLE biasanya digunakan baik untuk penaksir kemungkinan maksimum dan estimasi kemungkinan maksimum dengan konteks yang menunjukkan pilihan yang sesuai.
1.36 estimation : perkiraan
prosedur yang memperoleh representasi statistik dari suatu populasi (1.1) dari sampel acak (1.6) yang diambil dari populasi ini
Catatan :
- 1 : Secara khusus, prosedur yang terlibat dalam kemajuan dari penaksir (1.12) ke penduga khusus (1.31) merupakan pendugaan.
- 2 : Estimasi dipahami dalam konteks yang agak luas untuk memasukkan estimasi titik, estimasi interval atau estimasi properti populasi.
- 3 : Seringkali, representasi statistik mengacu pada estimasi parameter (2.9) atau parameter atau fungsi parameter dari model yang diasumsikan. Secara lebih umum, representasi populasi bisa jadi kurang spesifik, seperti statistik yang terkait dengan dampak bencana alam (korban, cedera, kerugian properti, dan kerugian pertanian — semuanya mungkin ingin diperkirakan oleh manajer darurat).
- 4 : Pertimbangan statistik deskriptif (1.5) dapat menunjukkan bahwa model yang diasumsikan memberikan representasi data yang tidak memadai, seperti yang ditunjukkan oleh ukuran kesesuaian model dengan data. Dalam kasus seperti itu, model lain dapat dipertimbangkan dan proses estimasi dilanjutkan.
Klausa 1.37 – 1.38
1.37 maximum likelihood estimation : estimasi kemungkinan maksimum
estimasi (1,36) berdasarkan estimator kemungkinan maksimum (1,35)
Catatan :
- 1 : Untuk distribusi normal (2,50), mean sampel (1,15) adalah penduga kemungkinan maksimum (1,35) dari parameter (2,9)μ sedangkan varians sampel (1,16), menggunakan penyebut n daripada n 1, memberikan penduga kemungkinan maksimum 2. Penyebut n 1 biasanya digunakan karena nilai ini memberikan penaksir tak bias (1,34).
- 2 : Estimasi kemungkinan maksimum kadang-kadang digunakan untuk menggambarkan penurunan penduga (1.12) dari fungsi kemungkinan.
- 3 : Meskipun dalam beberapa kasus, ekspresi bentuk tertutup muncul menggunakan estimasi kemungkinan maksimum, ada situasi lain di mana penaksir kemungkinan maksimum memerlukan solusi iteratif untuk satu set persamaan.
- 4 : Singkatan MLE biasanya digunakan baik untuk penaksir kemungkinan maksimum dan estimasi kemungkinan maksimum dengan konteks yang menunjukkan pilihan yang sesuai.
1.38 likelihood function : fungsi kemungkinan
fungsi kepadatan probabilitas (2,26) dievaluasi pada nilai yang diamati (1,4) dan dianggap sebagai fungsi dari parameter (2,9) dari keluarga distribusi (2,8)
CONTOH 1:
Pertimbangkan situasi di mana sepuluh item dipilih secara acak dari populasi yang sangat besar (1.1) dan 3 item ditemukan memiliki karakteristik tertentu. Dari sampel ini, perkiraan intuitif (1,31) dari proporsi populasi yang memiliki karakteristik adalah 0,3 (3 dari 10). Di bawah model distribusi binomial (2,46), fungsi kemungkinan (fungsi massa probabilitas sebagai fungsi p dengan n tetap pada 10 dan x pada 3) mencapai maksimum pada p = 0,3, sehingga sesuai dengan intuisi.
[Ini dapat diverifikasi lebih lanjut dengan memplot fungsi massa probabilitas dari distribusi binomial (2,46) 120 p3 (1 p) 7 versus p.]
CONTOH 2:
Untuk distribusi normal (2,50) dengan standar deviasi yang diketahui (2,37), dapat ditunjukkan secara umum bahwa fungsi kemungkinan mengambil maksimum pada sama dengan rata-rata sampel.
Klausa 1.39 – 1.40
1.39 profile likelihood function
fungsi kemungkinan profil
fungsi kemungkinan (1.38) sebagai fungsi dari parameter tunggal (2.9) dengan semua parameter lain diatur untuk memaksimalkannya
1.40 hypothesis (H) : hipotesa
pernyataan tentang populasi (1.1)
- Catatan 1 : Umumnya pernyataan tentang populasi menyangkut satu atau lebih parameter (2.9) dalam keluarga distribusi (2.8) atau tentang keluarga distribusi.
ISO 3534-1:2006 Klausa 1.41
Dikarenakan isi Klausa 1 dan 2 ini terlalu panjang, maka pembaca bisa melanjutkan ke artikel lanjutan dari standarku.com berikut :
- ISO 3534-1 klausa 1.41 – 1.65
Penutup
Demikian artikel dari standarku.com mengenai Standar ISO 3534-1:2006.
Mohon saran dari pembaca untuk kelengkapan isi artikel ini, silahkan saran tersebut dapat disampaikan melalui kolom komentar.
Baca artikel lain :
- International Organization for Standardization
- Memahami apa itu Standar ISO
- Memahami Standard atau Standar
Sumber referensi :