ISO 3534-1:2006 Klausa 1.1 – 1.20 adalah Standar Internasional mengenai kosakata dan simbol statistik, khususnya tentang istilah statistik umum dan istilah yang digunakan dalam probabilitas.
Artikel ini merupakan lanjutan dari artikel sebelumnya berikut :
- ISO 3534-1 istilah probabilitas statistik
ISO 3534-1:2006 Klausa 1.1 – 1.20
1 General statistical terms : Istilah statistik umum
ISO 3534-1:2006 Klausa 1.1 – 1.3
1.1 population : populasi
totalitas item dalam pertimbangan
Catatan :
- 1 : Suatu populasi mungkin nyata dan terbatas, nyata dan tak terbatas atau sepenuhnya hipotetis. Terkadang istilah “populasi terbatas” digunakan, terutama dalam pengambilan sampel survei. Demikian juga istilah “populasi tak terbatas” digunakan dalam konteks pengambilan sampel dari sebuah kontinum. Dalam Klausul 2, populasi akan dilihat dalam konteks probabilistik sebagai ruang sampel (2.1).
- 2 : Sebuah populasi hipotetis memungkinkan seseorang untuk membayangkan sifat data lebih lanjut di bawah berbagai asumsi. Oleh karena itu, populasi hipotetis berguna pada tahap desain penyelidikan statistik, terutama untuk menentukan ukuran sampel yang sesuai. Sebuah populasi hipotetis bisa terbatas atau tak terbatas jumlahnya. Ini adalah konsep yang sangat berguna dalam statistik inferensial untuk membantu mengevaluasi kekuatan bukti dalam penyelidikan statistik.
- 3 : Konteks investigasi dapat menentukan sifat populasi. Misalnya, jika tiga desa dipilih untuk studi demografi atau kesehatan, maka populasinya terdiri dari penduduk desa-desa tersebut. Atau, jika tiga desa dipilih secara acak dari semua desa di wilayah tertentu, maka populasinya akan terdiri dari semua penduduk wilayah tersebut.
1.2 sampling unit : unit pengambilan sampel
salah satu bagian individu di mana populasi (1.1) dibagi
- Catatan 1 : Tergantung pada keadaannya, bagian terkecil yang menarik mungkin adalah individu, rumah tangga, distrik sekolah, unit administrasi, dan sebagainya.
1.3 sample : Sampel
subset dari populasi (1.1) yang terdiri dari satu atau lebih unit sampling (1.2)
Catatan :
- 1 : Unit pengambilan sampel dapat berupa item, nilai numerik, atau bahkan entitas abstrak tergantung pada populasi yang diinginkan.
- 2 : Definisi sampel dalam ISO 3534-2 mencakup contoh kerangka sampel yang penting dalam menggambar sampel acak dari populasi terbatas.
ISO 3534-1:2006 Klausa 1.4 – 1.5
1.4 observed value : nilai yang diamati
nilai yang diperoleh dari properti yang terkait dengan satu anggota sampel (1.3)
Catatan :
- 1 : Sinonim umum adalah “realisasi” dan “datum”. Bentuk jamak dari datum adalah data.
- 2 : Definisi tidak menentukan asal-usul atau bagaimana nilai ini diperoleh. Nilai dapat mewakili satu realisasi dari variabel acak (2.10), tetapi tidak secara eksklusif demikian. Ini mungkin salah satu dari beberapa nilai yang selanjutnya akan dikenakan analisis statistik. Meskipun kesimpulan yang tepat memerlukan beberapa dasar statistik, tidak ada yang menghalangi ringkasan komputasi atau penggambaran grafis dari nilai yang diamati. Hanya ketika isu-isu yang menyertai seperti menentukan probabilitas mengamati serangkaian realisasi tertentu, mesin statistik menjadi relevan dan esensial. Tahap awal analisis nilai yang diamati biasanya disebut sebagai analisis data.
1.5 descriptive statistics : Statistik deskriptif
penggambaran grafik, numerik, atau ringkasan lainnya dari nilai-nilai yang diamati (1.4)
CONTOH
- 1: Ringkasan numerik meliputi rata-rata (1,15), rentang sampel (1,10), standar deviasi sampel (1,17), dan seterusnya.
- 2: Contoh ringkasan grafis termasuk boxplot, diagram, plot Q-Q, plot kuantil normal, scatterplot, beberapa scatterplot dan histogram.
ISO 3534-1:2006 Klausa 1.6 – 1.7
1.6 random sample : contoh acak
sampel (1.3) yang telah dipilih dengan metode pemilihan acak
Catatan :
- 1 : Definisi ini kurang restriktif daripada yang diberikan dalam ISO 3534-2 untuk memungkinkan populasi tak terbatas.
- 2 : Ketika sampel dari n unit sampling dipilih dari ruang sampel berhingga (2.1), masing-masing kemungkinan kombinasi dari n unit sampling akan memiliki probabilitas tertentu (2.5) untuk diambil. Untuk rencana pengambilan sampel survei, probabilitas khusus untuk setiap kombinasi yang mungkin dapat dihitung terlebih dahulu.
- 3 : Untuk pengambilan sampel survei dari ruang sampel terbatas, sampel acak dapat dipilih dengan rencana pengambilan sampel yang berbeda seperti pengambilan sampel acak berlapis, pengambilan sampel acak sistematis, pengambilan sampel cluster, pengambilan sampel dengan probabilitas pengambilan sampel yang proporsional dengan ukuran variabel tambahan dan banyak kemungkinan lainnya.
- 4 : Definisi umumnya mengacu pada nilai pengamatan aktual (1.4). Nilai-nilai yang diamati ini dianggap sebagai realisasi variabel acak (2.10), di mana setiap nilai yang diamati sesuai dengan satu variabel acak. Ketika penduga (1,12), statistik uji untuk uji statistik (1,48) atau interval kepercayaan (1,28) diturunkan dari sampel acak, definisi mengakomodasi referensi ke variabel acak yang muncul dari entitas abstrak dalam sampel daripada nilai pengamatan aktual dari variabel acak tersebut. variabel acak.
- 5 : Sampel acak dari populasi tak terbatas sering dihasilkan dengan penarikan berulang dari ruang sampel, yang mengarah ke sampel yang terdiri dari variabel acak independen yang terdistribusi secara identik menggunakan interpretasi definisi yang disebutkan dalam Catatan 4.
1.7 simple random sample : sampel acak sederhana
sampel acak (1.6) sedemikian rupa sehingga setiap subset dari ukuran tertentu memiliki probabilitas pemilihan yang sama
- Catatan 1 : Definisi ini selaras dengan definisi yang diberikan dalam ISO 3534-2, meskipun kata-katanya di sini sedikit berbeda.
ISO 3534-1:2006 Klausa 1.8
1.8 statistic : statistik
fungsi yang ditentukan sepenuhnya dari variabel acak (2.10)
Catatan :
- 1 : Statistik adalah fungsi dari variabel acak dalam sampel acak (1.6) dalam pengertian yang diberikan dalam Catatan 4 dari 1.6.
- 2 : Mengacu pada Catatan 1, jika {X1, X2, …, Xn} adalah sampel acak dari distribusi normal (2,50) dengan mean tidak diketahui (2,35) dan simpangan baku tidak diketahui (2,37)σ, maka ekspresi (X1 + X2 + … + Xn)/n adalah statistik, mean sampel (1,15), sedangkan [(X1 + X2 + … + Xn)/n] bukan statistik seperti itu melibatkan nilai parameter yang tidak diketahui (2.9)μ.
- 3 : Definisi yang diberikan di sini adalah definisi teknis, sesuai dengan perlakuan yang ditemukan dalam statistik matematika. Dalam pengaturan aplikasi, bentuk jamak dari statistik, yaitu statistik, dapat merujuk pada disiplin teknis yang melibatkan kegiatan analisis yang dijelaskan dalam Standar Internasional ISO/TC 69.
ISO 3534-1:2006 Klausa 1.9
1.9 order statistic : statistik pesanan
statistik (1.8) ditentukan oleh peringkatnya dalam pengaturan variabel acak yang tidak menurun (2.10)
CONTOH:
- Misalkan nilai-nilai yang diamati dari suatu sampel adalah 9, 13, 7, 6, 13, 7, 19, 6, 10, dan 7. Nilai-nilai yang diamati dari statistik urutan adalah 6, 6, 7, 7, 7, 9, 10 , 13, 13, 19. Nilai-nilai ini merupakan realisasi dari X(1) sampai X(10).
Catatan 1-4 :
- 1 : Biarkan nilai yang diamati (1.4) dari sampel acak (1.6) menjadi {x1, x2,…, xn} dan sekali diurutkan dalam urutan yang tidak menurun ditunjuk sebagai x(1) … x(k) … x(n). Maka (x(1),…, x(k),…, x(n) ) adalah nilai observasi dari statistik orde (X(1),…, X(k),…, X(n)) dan x(k) adalah nilai yang diamati dari statistik orde ke-k.
- 2 : Dalam istilah praktis, memperoleh statistik urutan untuk kumpulan data sama dengan menyortir data seperti yang dijelaskan secara formal dalam Catatan 1. Bentuk kumpulan data yang diurutkan kemudian cocok untuk memperoleh statistik ringkasan yang berguna seperti yang diberikan dalam beberapa berikut definisi.
- 3 : Statistik pesanan melibatkan nilai sampel yang diidentifikasi berdasarkan posisinya setelah peringkat dalam urutan yang tidak menurun. Seperti pada contoh, lebih mudah untuk memahami pengurutan nilai sampel (realisasi variabel acak) daripada pengurutan variabel acak yang tidak teramati. Namun demikian, seseorang dapat membayangkan variabel acak dari sampel acak (1,6) yang disusun dalam urutan yang tidak menurun. Misalnya, maksimum n variabel acak dapat dipelajari terlebih dahulu dari nilai realisasinya.
- 4 : Statistik orde individual adalah statistik yang merupakan fungsi yang ditentukan sepenuhnya dari variabel acak. Fungsi ini hanyalah fungsi identitas dengan identifikasi lebih lanjut dari posisi atau peringkat dalam himpunan variabel acak yang diurutkan.
Catatan 1-4 :
- 5 : Nilai terikat menimbulkan masalah potensial terutama untuk variabel acak diskrit dan untuk realisasi yang dilaporkan dengan resolusi rendah. Kata “tidak menurun” digunakan daripada “naik” sebagai pendekatan halus untuk masalah ini. Harus ditekankan bahwa nilai terikat dipertahankan dan tidak runtuh menjadi nilai terikat tunggal. Dalam contoh di atas, dua realisasi 6 dan 6 adalah nilai terikat.
- 6 : Pengurutan dilakukan dengan mengacu pada garis nyata dan bukan pada nilai absolut dari variabel acak.
- 7 : Kumpulan statistik orde lengkap terdiri dari variabel acak n dimensi, di mana n adalah jumlah pengamatan dalam sampel.
- 8 : Komponen statistik urutan juga disebut sebagai statistik urutan tetapi dengan kualifikasi yang memberikan nomor dalam urutan nilai sampel yang dipesan.
- 9 : Minimum, maksimum, dan untuk ukuran sampel bernomor ganjil, median sampel (1,13), adalah kasus khusus dari statistik pesanan. Misalnya, untuk ukuran sampel 11, X(1) adalah minimum, X(11) adalah maksimum dan X(6) adalah median sampel.
ISO 3534-1:2006 Klausa 1.10 – 1.12
1.10 sample range : rentang sampel
statistik orde terbesar (1.9) dikurangi statistik orde terkecil
CONTOH:
Melanjutkan contoh dari 1.9, rentang sampel yang diamati adalah 19 6 = 13.
- Catatan 1 : Dalam pengendalian proses statistik, rentang sampel sering digunakan untuk memantau dispersi dari waktu ke waktu suatu proses, terutama ketika ukuran sampel relatif kecil.
1.11 mid-range : menengah
rata-rata (1,15) statistik orde terkecil dan terbesar (1,9)
CONTOH:
Rentang tengah yang diamati untuk nilai contoh dalam 1,9 adalah (6+19)/2 = 12,5.
- Catatan 1 : Rentang menengah memberikan penilaian cepat dan sederhana dari kumpulan data kecil tengah.
1.12 estimator : penaksir
statistik (1,8) yang digunakan dalam estimasi (1,36) parameter
Catatan :
- 1 : Penaksir dapat berupa rata-rata sampel (1,15) yang dimaksudkan untuk memperkirakan rata-rata populasi (2,35), yang dapat dilambangkan dengan . Untuk distribusi (2.11) seperti distribusi normal (2.50), penduga “alami” dari rata-rata populasi adalah rata-rata sampel.
- 2 : Untuk memperkirakan properti populasi [mis. mode (2.27) untuk distribusi univariat (2.16)], estimator yang sesuai bisa menjadi fungsi dari estimator dari parameter distribusi atau bisa menjadi fungsi kompleks dari sampel acak (1.6).
- 3 : Istilah “penaksir” digunakan di sini dalam arti luas. Ini termasuk estimator titik untuk parameter, serta estimator interval yang mungkin digunakan untuk prediksi (kadang-kadang disebut sebagai prediktor). Penaksir juga dapat menyertakan fungsi seperti penaksir kernel dan statistik tujuan khusus lainnya. Pembahasan tambahan diberikan dalam catatan 1.36.
ISO 3534-1:2006 Klausa 1.13
1.13 sample median : contoh median
[(n+1)/2]statistik urutan ke-(1.9), jika ukuran sampel (lihat ISO 3534-2:2006, 1.2.26) n ganjil; jumlah statistik orde ke (n/2) dan [(n/2) + 1] dibagi 2, jika ukuran sampel n genap
CONTOH:
Melanjutkan contoh 1.9, nilai 8 merupakan realisasi dari median sampel. Dalam kasus ini (bahkan ukuran sampel 10), nilai ke-5 dan ke-6 adalah 7 dan 9, yang rata-ratanya sama dengan 8. Dalam praktiknya, ini akan dilaporkan sebagai “median sampel adalah 8”, meskipun sebenarnya median sampel adalah didefinisikan sebagai variabel acak.
Catatan :
- 1 : Untuk sampel acak (1.6) dengan ukuran sampel n yang variabel acaknya (2.10) disusun dalam urutan yang tidak menurun dari 1 hingga n, median sampel adalah (n+1)/2 variabel acak jika ukuran sampel ganjil. Jika ukuran sampel n genap, maka median sampel adalah rata-rata dari (n/2) dan (n+1)/2 variabel acak.
- 2 : Secara konseptual, tampaknya mustahil untuk melakukan pengurutan variabel acak yang belum diamati. Namun demikian, struktur untuk memahami statistik keteraturan dapat ditetapkan sehingga setelah pengamatan, analisis dapat dilanjutkan. Dalam praktiknya, seseorang memperoleh nilai yang diamati dan melalui pengurutan nilai, seseorang memperoleh realisasi statistik urutan. Realisasi ini kemudian dapat diinterpretasikan dari struktur statistik pesanan dari sampel acak.
- 3 : Median sampel menyediakan penaksir tengah distribusi, dengan setengah sampel di setiap sisinya.
- 4 : Dalam praktiknya, median sampel berguna dalam menyediakan penduga yang tidak sensitif terhadap nilai yang sangat ekstrem dalam kumpulan data. Misalnya, pendapatan rata-rata dan harga rumah rata-rata sering dilaporkan sebagai nilai ringkasan.
Klausa 1.14
1.14 sample moment of order k : contoh momen orde k
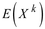
jumlah pangkat k variabel acak (2,10) dalam sampel acak (1,6) dibagi dengan jumlah pengamatan dalam sampel (1,3)
Catatan :
- 1 : Untuk sampel acak dengan ukuran sampel n, yaitu {X1, X2, …, Xn}, momen sampel orde k, E(Xk), adalah
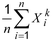
- 2 : Selanjutnya, konsep ini dapat digambarkan sebagai momen sampel orde k tentang nol.
- 3 : Momen sampel orde 1 akan terlihat pada definisi berikutnya sebagai mean sampel (1,15).
- Catatan 4 : Meskipun definisi diberikan untuk k sewenang-wenang, contoh yang umum digunakan dalam praktik melibatkan k = 1 [rata-rata sampel (1,15)], k = 2 [dikaitkan dengan varians sampel (1,16) dan standar deviasi sampel (1,17) ], k = 3 [terkait dengan koefisien skewness sampel (1,20)] dan k = 4 [terkait dengan koefisien sampel kurtosis (1,21)].
- Catatan 5 : “E” di berasal dari “nilai yang diharapkan” atau “harapan” dari variabel acak X.
Klausa 1.15
1.15 sample mean : sampel berarti
average : rata-rata
arithmetic mean : rata-rata aritmatika
jumlah variabel acak (2,10) dalam sampel acak (1,6) dibagi dengan jumlah suku dalam jumlah
CONTOH:
Melanjutkan contoh dari 1,9, realisasi mean sampel adalah 9,7 karena jumlah nilai yang diamati adalah 97 dan ukuran sampel adalah 10.
Catatan :
- 1 : Dianggap sebagai statistik, mean sampel adalah fungsi dari variabel acak dari sampel acak dalam pengertian yang diberikan dalam Catatan 3 dari 1.8. Seseorang harus membedakan penduga ini dari nilai numerik rata-rata sampel yang dihitung dari nilai yang diamati (1,4) dalam sampel acak.
- 2 : Rata-rata sampel yang dianggap sebagai statistik sering digunakan sebagai penaksir untuk rata-rata populasi (2,35). Sinonim yang umum adalah mean aritmatika.
- 3 : Untuk sampel acak dengan ukuran sampel n, yaitu {X1, X2, …, Xn}, mean sampel adalah:
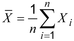
- 4 : Rata-rata sampel dapat dikenali sebagai momen sampel orde 1.
- 5 : Untuk ukuran sampel 2, rata-rata sampel, median sampel (1.13) dan rentang tengah (1.11) adalah sama.
Klausa 1.16 – 1.17
1.16 sample variance (S2) : varians sampel
jumlah deviasi kuadrat dari variabel acak (2,10) dalam sampel acak (1,6) dari rata-rata sampelnya (1,15) dibagi dengan jumlah suku dalam jumlah dikurangi satu
CONTOH:
Melanjutkan dengan contoh numerik 1,9, varians sampel dapat dihitung menjadi 17,57. Jumlah kuadrat dari rata-rata sampel yang diamati adalah 158,10 dan ukuran sampel 10 dikurangi 1 adalah 9, memberikan penyebut yang sesuai.
Catatan :
- 1 : Dianggap sebagai statistik (1.8), varians sampel S2 adalah fungsi dari variabel acak dari sampel acak. Kita harus membedakan estimator ini (1,12) dari nilai numerik dari varians sampel yang dihitung dari nilai-nilai yang diamati (1,4) dalam sampel acak. Nilai numerik ini disebut varians sampel empiris atau varians sampel yang diamati dan biasanya dilambangkan dengan s2.
- 2 : Untuk sampel acak dengan ukuran sampel n, yaitu {X1, X2, …, Xn} dengan mean sampel, varians sampel adalah:
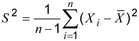
- 3 : Varians sampel adalah statistik yang “hampir” merupakan rata-rata deviasi kuadrat dari variabel acak (2.10) dari rata-rata sampelnya (hanya “hampir” karena n 1 digunakan daripada n dalam penyebut ). Menggunakan n 1 memberikan penduga tak bias (1,34) dari varians populasi (2,36).
- 4 : Kuantitas n 1 dikenal sebagai derajat kebebasan (2,54).
- 5 : Varians sampel dapat dikenali sebagai momen sampel ke-2 dari variabel acak sampel standar (1,19).
1.17 sample standard deviation (S) : standar deviasi sampel
akar kuadrat non-negatif dari varians sampel (1,16)
CONTOH:
Melanjutkan contoh numerik 1,9, standar deviasi sampel yang diamati adalah 4.192 karena varians sampel yang diamati adalah 17,57.
Catatan :
- 1 : Dalam praktiknya, simpangan baku sampel digunakan untuk memperkirakan simpangan baku (2,37). Di sini sekali lagi, perlu ditekankan bahwa S juga merupakan variabel acak (2.10) dan bukan realisasi dari sampel acak (1.6).
- 2 : Simpangan baku sampel adalah ukuran penyebaran suatu distribusi (2.11).
Klausa 1.18 – 1.19
1.18 sample coefficient of variation : koefisien variasi sampel
simpangan baku sampel (1,17) dibagi rata-rata sampel (1,15)
- Catatan 1 : Seperti halnya koefisien variasi (2,38), kegunaan statistik ini terbatas pada populasi yang bernilai positif. Koefisien variasi sampel biasanya dilaporkan sebagai persentase. Hal ini terutama berlaku di mana variasi meningkat sebanding dengan rata-rata.
1.19 standardized sample random variable : variabel acak sampel standar
variabel acak (2,10) dikurangi mean sampelnya (1,15) dibagi dengan standar deviasi sampel (1,17)
CONTOH:
Untuk contoh 1,9, mean sampel yang diamati adalah 9,7 dan standar deviasi sampel yang diamati adalah 4,192. Oleh karena itu, variabel acak standar yang diamati (sampai dua tempat desimal) adalah:
0,17; 0,79; 0,64; 0,88; 0,79; 0,64; 2,22; 0,88; 0,07; 0,64.
Catatan :
- 1 : Variabel acak sampel standar dibedakan dari variabel acak standar mitra teoritisnya (2,33). Maksud dari standardisasi adalah untuk mengubah variabel acak menjadi nol rata-rata dan standar deviasi unit, untuk kemudahan dalam interpretasi dan perbandingan.
- 2 : Nilai pengamatan standar memiliki rata-rata pengamatan nol dan simpangan baku teramati 1.
ISO 3534-1:2006 Klausa 1.20
1.20 sample coefficient of skewness : sampel koefisien kemiringan
rata-rata aritmatika pangkat ketiga dari variabel acak sampel standar (1,19) dari sampel acak (1,6)
CONTOH:
Melanjutkan contoh dari 1.9, koefisien skewness sampel yang diamati dapat dihitung menjadi 0,971 88. Untuk ukuran sampel seperti 10 dalam contoh ini, koefisien skewness sampel sangat bervariasi, sehingga harus digunakan dengan hati-hati. Menggunakan rumus alternatif di Catatan 1, nilai yang dihitung adalah 1.349 83.
Catatan :
- 1 : Rumus yang sesuai dengan definisi adalah
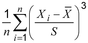
Beberapa paket statistik menggunakan rumus berikut untuk koefisien skewness sampel untuk mengoreksi bias (1,33):
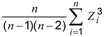
di mana
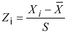
Untuk ukuran sampel yang besar, perbedaan antara kedua perkiraan dapat diabaikan. Rasio tak bias terhadap estimasi bias adalah 1,389 untuk n = 10, 1,031 untuk n = 100 dan 1,003 untuk n = 1 000.
- 2 : Kemiringan mengacu pada kurangnya simetri. Nilai statistik ini mendekati nol menunjukkan bahwa distribusi yang mendasari kira-kira simetris, sedangkan nilai bukan nol kemungkinan akan sesuai dengan distribusi yang memiliki nilai ekstrim sesekali di satu sisi pusat distribusi. Data miring juga akan tercermin dalam nilai mean sampel (1,15) dan median sampel (1,13) yang tidak serupa. Data yang condong positif (right-skewed) menunjukkan kemungkinan adanya beberapa pengamatan besar yang ekstrem. Demikian pula, data condong negatif (miring kiri) menunjukkan kemungkinan adanya beberapa pengamatan kecil yang ekstrem.
- 3 : Koefisien kemiringan sampel dapat dikenali sebagai momen sampel ke-3 dari variabel acak sampel standar (1,19).
ISO 3534-1:2006 Klausa 1.21
Dikarenakan isi Klausa 1 dan 2 ini terlalu panjang, maka pembaca bisa melanjutkan ke artikel lanjutan dari standarku.com berikut :
- ISO 3534-1 klausa 1.21 – 1.40
Penutup
Demikian artikel dari standarku.com mengenai Standar ISO 3534-1:2006.
Mohon saran dari pembaca untuk kelengkapan isi artikel ini, silahkan saran tersebut dapat disampaikan melalui kolom komentar.
Baca artikel lain :
- International Organization for Standardization
- Memahami apa itu Standar ISO
- Memahami Standard atau Standar
Sumber referensi :