ISO 3534-2:2006 Klausa 2.5 – 2.7 adalah Standar Internasional mengenai statistik, khususnya tentang kosakata dan simbol untuk statistik terapan.
Artikel ini merupakan lanjutan dari artikel sebelumnya berikut :
ISO 3534-2:2006 Klausa 2.5 – 2.7
2.5 Fundamental terms related to process performance and process capability : Istilah dasar yang terkait dengan kinerja proses dan kemampuan proses
ISO 3534-2:2006 Klausa 2.5.1 – 2.5.3
2.5.1 distribution : distribusi
informasi tentang perilaku probabilistik suatu karakteristik (1.1.1)
Catatan :
- 1 : Distribusi suatu karakteristik dapat direpresentasikan, misalnya, dengan memberi peringkat pada nilai-nilai karakteristik dan menunjukkan pola pengukuran atau skor yang dihasilkan dalam bentuk bagan penghitungan atau histogram. Pola seperti itu memberikan semua informasi nilai numerik pada karakteristik kecuali untuk urutan serial di mana data muncul.
- 2 : Distribusi karakteristik tergantung pada kondisi yang berlaku. Jadi, jika informasi yang berarti tentang distribusi karakteristik yang diinginkan, kondisi di mana data dikumpulkan harus ditentukan.
- 3 : Penting untuk mengetahui kelas distribusi (2.5.2), misalnya, normal atau log-normal, sebelum memprediksi atau memperkirakan kemampuan proses dan ukuran kinerja dan indeks atau fraksi yang tidak sesuai.
2.5.2 class of distributions : kelas distribusi
keluarga distribusi tertentu (2.5.1) yang masing-masing anggotanya memiliki atribut umum yang sama yang dengannya keluarga tersebut sepenuhnya ditentukan
Contoh :
- 1: Dua parameter, berbentuk lonceng simetris, berdistribusi normal dengan parameter mean dan standar deviasi.
- 2: Distribusi Weibull tiga parameter dengan parameter lokasi, bentuk dan skala (1.1.3).
- 3: Distribusi kontinu unimodal.
Catatan 1 :
- Kelas distribusi seringkali dapat ditentukan sepenuhnya melalui nilai parameter yang sesuai.
2.5.3 distribution model : model distribusi
distribusi tertentu (2.5.1) atau kelas distribusi (2.5.2)
Contoh :
- 1: Sebuah model untuk distribusi karakteristik produk (1.1.1), diameter baut, mungkin distribusi normal dengan rata-rata 15 mm dan standar deviasi 0,05 mm. Di sini modelnya sepenuhnya ditentukan.
- 2: Sebuah model untuk diameter baut seperti pada Contoh 1 dapat menjadi kelas distribusi normal tanpa mencoba untuk menentukan distribusi tertentu. Di sini model adalah kelas dari distribusi normal.
ISO 3534-2:2006 Klausa 2.5.4 – 2.5.5
2.5.4 upper fraction nonconforming (pU) : pecahan atas tidak sesuai
fraksi distribusi (2.5.1) dari karakteristik (1.1.1) yang lebih besar dari batas spesifikasi atas (3.1.4), U
Contoh :
- Dalam distribusi normal dengan mean, μ, dan standar deviasi, σ:
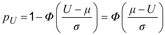
di mana :
- pU adalah pecahan atas yang tidak sesuai;
- Φ adalah fungsi distribusi dari distribusi normal standar (lihat ISO 3534-1);
- U adalah batas spesifikasi atas.
Catatan :
- 1 : Tabel (atau fungsi dalam paket komputer statistik) dari distribusi normal standar sudah tersedia yang memberikan proporsi output proses yang diharapkan melebihi nilai tertentu yang diinginkan, seperti batas spesifikasi (3.1.3), dalam istilah simpangan baku jauh dari rata-rata proses. Ini meniadakan kebutuhan untuk mengerjakan fungsi distribusi statistik yang diberikan dalam contoh.
- 2 : Fungsi berhubungan dengan distribusi teoretis. Dalam praktiknya, dengan distribusi empiris, parameter diganti dengan perkiraannya.
2.5.5 lower fraction nonconforming (pL) : pecahan bawah tidak sesuai
fraksi distribusi (2.5.1) dari karakteristik (1.1.1) yang kurang dari batas spesifikasi bawah (3.1.5), L
Contoh :
Dalam distribusi normal dengan mean, μ, dan standar deviasi, σ:
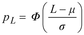
di mana :
- pL adalah pecahan bawah yang tidak sesuai;
- Φ adalah fungsi distribusi dari distribusi normal standar;
- L adalah batas spesifikasi bawah.
Catatan :
- 1 : Tabel (atau fungsi dalam paket komputer statistik) dari distribusi normal standar sudah tersedia yang memberikan proporsi output proses yang diharapkan melebihi nilai tertentu yang diinginkan, seperti batas spesifikasi (3.1.3), dalam istilah simpangan baku jauh dari rata-rata proses. Ini meniadakan kebutuhan untuk mengerjakan fungsi distribusi statistik yang diberikan dalam contoh.
- 2 : Fungsi berhubungan dengan distribusi teoretis. Dalam praktiknya, dengan distribusi empiris, parameter diganti dengan perkiraannya.
ISO 3534-2:2006 Klausa 2.5.6 – 2.5.7
2.5.6 total fraction nonconforming (pt) : pecahan total tidak sesuai
jumlah pecahan atas yang tidak sesuai (2.5.4) dan pecahan bawah yang tidak sesuai (2.5.5)
Contoh : Pada distribusi normal (2.5.1) dengan mean,μ, dan simpangan baku, σ:
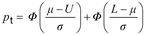
di mana :
- pt adalah pecahan total yang tidak sesuai;
- Φ adalah fungsi distribusi dari distribusi normal standar;
- L adalah batas spesifikasi bawah;
- U adalah batas spesifikasi atas.
Catatan :
- 1 : Tabel (atau fungsi dalam paket komputer statistik) dari distribusi normal standar sudah tersedia yang memberikan proporsi output proses yang diharapkan melebihi nilai tertentu yang diinginkan, seperti batas spesifikasi (3.1.3), dalam istilah simpangan baku jauh dari rata-rata proses. Ini meniadakan kebutuhan untuk mengerjakan fungsi distribusi statistik yang diberikan dalam contoh.
- 2 : Fungsi berhubungan dengan distribusi teoretis. Dalam praktiknya, dengan distribusi empiris, parameter diganti dengan perkiraannya.
2.5.7 reference interval : interval referensi
interval dibatasi oleh kuantil distribusi 99,865 %, X99,865 %, dan kuantil distribusi 0,135 %, X0,135 %
Catatan :
- 1 : Interval dapat dinyatakan dengan (X99,865 %, X0,135 %) dan panjang interval adalah X99,865 % X0,135 %
- 2 : Istilah ini hanya digunakan sebagai dasar yang sewenang-wenang, tetapi standar, untuk mendefinisikan indeks kinerja proses (2.6.2) dan indeks kapabilitas proses (2.7.2).
- 3 : Untuk distribusi normal (2.5.1), panjang interval referensi dapat dinyatakan dalam enam standar deviasi, 6σ, atau 6S, bila diperkirakan dari sampel.
- 4 : Untuk distribusi non-normal, panjang interval referensi dapat diperkirakan dengan menggunakan kertas probabilitas yang sesuai (misalnya log-normal) atau dari sampel kurtosis dan kemiringan sampel menggunakan metode yang dijelaskan dalam ISO/TR 127831 ).
- 5 : Kuantil atau fraktil menunjukkan pembagian distribusi menjadi unit yang sama (1.2.14) atau pecahan, mis. persentil. Kuantil didefinisikan dalam ISO 3534-1.
ISO 3534-2:2006 Klausa 2.5.8 – 2.5.9
2.5.8 lower reference interval : interval referensi yang lebih rendah
interval dibatasi oleh kuantil distribusi 50 %, X50 % dan kuantil distribusi 0,135 %, X0,135 %
Catatan :
- 1 : Interval dapat dinyatakan dengan (X50 %, X0,135%) dan panjang interval adalah X50 % X0,135 %.
- 2 : Istilah ini hanya digunakan sebagai dasar yang sewenang-wenang, tetapi standar, untuk menentukan indeks kinerja proses yang lebih rendah (2.6.3) dan indeks kapabilitas proses yang lebih rendah (2.7.3).
- 3 : Untuk distribusi normal (2.5.1), panjang interval referensi yang lebih rendah dapat dinyatakan dalam standar deviasi sebagai 3σ, atau perkiraan 3S, dan X50 % mewakili mean dan median.
- 4 : Untuk distribusi non-normal, kuantil distribusi 50%, X50 %, yaitu median, dan kuantil distribusi 0,135%, X0,135% dapat diperkirakan dengan menggunakan kertas probabilitas yang sesuai (misalnya log-normal ) atau dari sampel kurtosis dan kemiringan sampel menggunakan metode yang dijelaskan dalam ISO/TR 127831).
2.5.9 upper reference interval : interval referensi atas
interval dibatasi oleh kuantil distribusi 99,865%, X99,865 %, dan kuantil distribusi 50%, X50 %
Catatan :
- 1 : Interval dapat dinyatakan dengan (X99,865 %, X50 %) dan panjang interval adalah X99,865 % X50 %.
- 2 : Istilah ini hanya digunakan sebagai dasar yang sewenang-wenang, tetapi standar, untuk menentukan indeks kinerja proses atas (2.6.4) dan indeks kemampuan proses atas (2.7.4).
- 3 : Untuk distribusi normal (2.5.1), panjang interval referensi atas dapat dinyatakan dalam standar deviasi sebagai 3σ, atau perkiraan 3S, dan X50 % mewakili mean dan median.
- 4 : Untuk distribusi non-normal, kuantil distribusi 50%, X50%, yaitu median, dan kuantil distribusi 99,865%, X99,865%, dapat diperkirakan dengan menggunakan kertas probabilitas yang sesuai (misalnya log- normal) atau dari sampel kurtosis dan kemiringan sampel menggunakan metode yang dijelaskan dalam ISO/TR 127832).
2.6 Process performance {measured data} : {Kinerja proses data terukur}
ISO 3534-2:2006 Klausa 2.6.1
2.6.1 process performance : kinerja proses
ukuran statistik dari hasil suatu karakteristik (1.1.1) dari suatu proses (2.1.1) yang mungkin tidak dapat dibuktikan berada dalam keadaan kendali statistik (2.2.7)
Catatan :
1 : Hasilnya adalah distribusi (2.5.1) kelas (2.5.2) yang perlu ditentukan dan parameternya dinilai.
2 : Kehati-hatian harus dilakukan dalam menggunakan ukuran ini karena dapat mengandung komponen variabilitas karena penyebab khusus (2.2.4), yang nilainya tidak dapat diprediksi.
3 : Untuk distribusi normal yang dijelaskan dalam hal standar deviasi, St, dinilai dari hanya satu sampel (1.2.17) ukuran N, standar deviasi proses dinyatakan sebagai berikut:
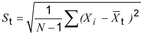
di mana,
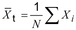
Deskriptor ini, St, memperhitungkan variasi (2.2.1) karena penyebab acak (umum) (2.2.5) bersama dengan penyebab khusus yang mungkin ada. St digunakan di sini sebagai ganti t, karena standar deviasi adalah ukuran deskriptif statistik. Ukuran sampel N dapat terdiri dari k subkelompok, masing-masing berukuran n.
4 : Untuk distribusi normal, kinerja proses dapat dinilai dari ekspresi:
dan, “z” tergantung pada bagian tertentu per juta persyaratan kinerja. Biasanya “z” mengambil nilai 3, 4 atau 5. Jika kinerja proses bertepatan dengan persyaratan yang ditentukan, nilai z 3 menunjukkan 2 700 bagian per juta yang diharapkan di luar spesifikasi (3.1.1). Demikian pula, z dari 4 menunjukkan 64 bagian per juta yang diharapkan dan z dari 5 yang diharapkan 0,6 bagian per juta di luar spesifikasi.
5 : Untuk distribusi non-normal, kinerja proses dapat dinilai menggunakan, misalnya, kertas probabilitas yang sesuai atau dari parameter distribusi yang dipasang pada data. Ekspresi untuk kinerja proses mengambil bentuk:
Notasi , , memiliki gaya yang sama dengan praktik kantor menggambar standar untuk menyatakan toleransi yang ditentukan (3.1.6) tentang nilai nominal, atau nilai yang disukai, untuk suatu karakteristik ketika nilai yang disukai tidak berjarak sama dari setiap batas. Notasi ekivalen untuk batas simetris tentang nilai yang disukai adalah ±. Hal ini memungkinkan perbandingan langsung dibuat antara kinerja dimensi karakteristik dan persyaratan yang ditentukan baik dari segi lokasi dan dispersi.
ISO 3534-2:2006 Klausa 2.6.2 – 2.6.3
2.6.2 process performance index (Pp) : indeks kinerja proses
indeks yang menggambarkan kinerja proses (2.6.1) dalam kaitannya dengan toleransi yang ditentukan (3.1.6)
Catatan :
1 : Seringkali, indeks kinerja proses dinyatakan sebagai nilai toleransi yang ditentukan dibagi dengan ukuran panjang interval referensi (2.5.7), yaitu sebagai:
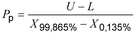
2 : Untuk distribusi normal (2.5.1), panjang interval referensi sama dengan 6 St (lihat 2.6.1, Catatan 3)
3 : Untuk distribusi non-normal, panjang interval referensi dapat diperkirakan menggunakan, misalnya, metode yang dijelaskan dalam ISO/TR 127833).
2.6.3 lower process performance index (PpkL) : indeks kinerja proses yang lebih rendah
indeks yang menggambarkan kinerja proses (2.6.1) dalam kaitannya dengan batas spesifikasi yang lebih rendah (3.1.5), L
Catatan :
1 : Seringkali, indeks kinerja proses yang lebih rendah dinyatakan dengan perbedaan antara kuantil distribusi 50%, X50 %, dan batas spesifikasi bawah (3.1.5) dibagi dengan ukuran panjang interval referensi yang lebih rendah (2.5 .8), yaitu sebagai:
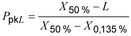
2 : Untuk distribusi normal simetris, panjang interval referensi bawah sama dengan 3St (lihat 2.6.1, Catatan 3) dan X50 % mewakili mean dan median.
3 : Untuk distribusi non-normal, panjang interval referensi yang lebih rendah dapat diperkirakan menggunakan metode yang dijelaskan dalam ISO/TR 127834) dan X50 % mewakili median.
Klausa 2.6.4 – 2.6.6
2.6.4 upper process performance index (PpkU) : indeks kinerja proses atas
indeks yang menggambarkan kinerja proses (2.6.1) dalam kaitannya dengan batas spesifikasi atas (3.1.4), U
Catatan :
1 : Seringkali, indeks kinerja proses atas dinyatakan sebagai perbedaan antara batas spesifikasi atas dan kuantil distribusi 50%, X50%,, dibagi dengan ukuran panjang interval referensi atas (2.5.9) , yaitu sebagai:
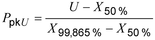
2 : Untuk distribusi normal, panjang interval referensi atas sama dengan 3 St (lihat 2.6.1, Catatan 3) dan X50 % mewakili mean dan median.
3 : Untuk distribusi non-normal, panjang interval referensi atas dapat diperkirakan menggunakan metode yang dijelaskan dalam ISO/TR 127834) dan X50 % mewakili median.
2.6.5 minimum process performance index (Ppk) : indeks kinerja proses minimum
lebih kecil dari indeks kinerja proses atas (2.6.4) dan indeks kinerja proses yang lebih rendah (2.6.3)
2.6.6 process performance ratio : rasio kinerja proses
kebalikan dari indeks kinerja proses (2.6.2)
- Catatan 1 : Rasio kinerja proses sering dinyatakan sebagai persentase.
2.7 Process capability {measured data} : {Kemampuan proses data terukur}
Klausa 2.7.1
2.7.1 process capability : kemampuan memproses
perkiraan statistik dari hasil suatu karakteristik (1.1.1) dari suatu proses (2.1.1) yang telah ditunjukkan berada dalam keadaan kendali statistik (2.2.7) dan yang menggambarkan kemampuan proses itu untuk mewujudkan suatu karakteristik yang akan memenuhi persyaratan untuk karakteristik itu
Catatan :
- 1 : Hasilnya adalah distribusi (2.5.1), kelas (2.5.2) yang perlu ditentukan dan parameternya diperkirakan.
- 2 : Untuk distribusi normal, standar deviasi keseluruhan proses, t, dapat diperkirakan menggunakan rumus untuk St (lihat 2.6.1, Catatan 3).
Alternatifnya, dalam keadaan tertentu, simpangan baku, Sw, yang hanya mewakili variasi dalam subgrup (2.2.1), dapat menggantikan St sebagai penduga.
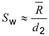
atau :
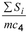
atau :
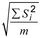
di mana :
- adalah rentang rata-rata yang dihitung dari sekumpulan m rentang subgrup;
- Si adalah fungsi distribusi dari distribusi normal standar (lihat ISO 3534-1);
- m adalah batas spesifikasi atas.
- d2, c4 adalah batas spesifikasi atas.
Nilai estimator St dan Sw konvergen untuk suatu proses dalam keadaan kendali statistik. Jadi, perbandingan keduanya memberikan indikasi tingkat stabilitas proses. Untuk proses di luar kendali tentang rata-rata konstan, atau, untuk proses yang tunduk pada perubahan sistematis rata-rata (lihat 2.2.7, Catatan 4), nilai Sw kemungkinan akan terlalu meremehkan standar deviasi proses .
Oleh karena itu Sw harus digunakan dengan sangat hati-hati. Kadang-kadang juga, penaksir St lebih disukai daripada Sw karena memiliki sifat statistik yang lebih dapat dilacak (misalnya memfasilitasi perhitungan batas kepercayaan).
3 : Untuk distribusi normal, kemampuan proses dapat dinilai dari ekspresi:

di mana :
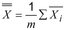
adalah rata-rata yang diamati dari subkelompok ke-i. Catatan yang memberikan hasil yang sama dengan (lihat 2.6.1, Catatan 3).
Pilihan nilai “z” tergantung pada bagian tertentu per juta standar kemampuan yang digunakan. Biasanya “z” mengambil nilai 3, 4 atau 5. Jika kemampuan proses memenuhi persyaratan yang ditentukan, nilai z 3 menunjukkan 2 700 bagian per juta yang diharapkan di luar spesifikasi (3.1.1). Demikian pula z dari 4 menunjukkan 64 bagian per juta yang diharapkan dan z dari 5 yang diharapkan 0,6 bagian per juta di luar spesifikasi.
4 :
Untuk distribusi non-normal, kemampuan proses dapat dinilai dengan menggunakan, misalnya, kertas probabilitas yang sesuai atau dari parameter distribusi yang sesuai dengan data. Ekspresi untuk kapabilitas proses mengambil bentuk asimetris:

Notasi tersebut,
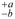
memiliki gaya yang sama dengan praktik kantor menggambar standar untuk menyatakan toleransi yang ditentukan (3.1.6) tentang nilai nominal, atau nilai yang disukai, untuk suatu karakteristik ketika nilai yang disukai tidak berjarak sama dari setiap batas. Notasi ekivalen untuk batas simetris tentang nilai yang disukai adalah ±. Hal ini memungkinkan perbandingan langsung dibuat antara kinerja dimensi karakteristik dan persyaratan yang ditentukan baik dari segi lokasi dan dispersi.
5 :
Ketika :
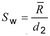
digunakan, perlu diperhatikan bahwa estimator ini:
- — menjadi semakin kurang efisien seiring bertambahnya ukuran subkelompok;
- — sangat sensitif terhadap distribusi individu;
- — membuatnya lebih sulit untuk memperkirakan batas keyakinan
Klausa 2.7.2 – 2.7.3
2.7.2 process capability index (Cp) : indeks kemampuan proses
indeks yang menggambarkan kemampuan proses (2.7.1) dalam kaitannya dengan toleransi yang ditentukan (3.1.6)
Catatan :
1 : Seringkali, indeks kapabilitas proses dinyatakan sebagai nilai toleransi yang ditentukan dibagi dengan ukuran panjang interval referensi (2.5.7) untuk proses dalam keadaan kontrol statistik (2.2.7) , yaitu sebagai:
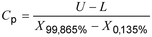
2 : Untuk distribusi normal, interval referensi sama dengan 6S (lihat 2.7.1, Catatan).
3 : Untuk distribusi non-normal, interval referensi dapat diperkirakan menggunakan metode yang dijelaskan dalam ISO/TR 127835).
2.7.3 lower process capability index (CpkL) : indeks kemampuan proses yang lebih rendah
indeks yang menggambarkan kemampuan proses (2.7.1) dalam kaitannya dengan batas spesifikasi yang lebih rendah (3.1.5), L
Catatan :
1 : Seringkali, indeks kapabilitas proses yang lebih rendah dinyatakan sebagai perbedaan antara kuantil distribusi 50%, X50%, dan batas spesifikasi bawah dibagi dengan ukuran panjang interval referensi yang lebih rendah (2.5.8) untuk proses dalam keadaan terkendali statistik (2.2.7), yaitu sebagai:
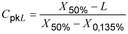
2 : Untuk distribusi normal, interval referensi yang lebih rendah sama dengan 3S (lihat 2.7.1, Catatan) dan X50 % mewakili mean dan median.
3 : Untuk distribusi non-normal, interval referensi yang lebih rendah dapat diperkirakan menggunakan metode yang dijelaskan dalam ISO/TR 127835) dan X50 % mewakili median.
Klausa 2.7.4 – 2.7.7
2.7.4 upper process capability index (CpkU) : indeks kemampuan proses atas
indeks yang menggambarkan kemampuan proses (2.7.1) dalam kaitannya dengan batas spesifikasi atas (3.1.4), U
Catatan :
1 : Seringkali, indeks kapabilitas proses atas dinyatakan sebagai perbedaan antara batas spesifikasi atas dan kuantil distribusi 50%, X50%, dibagi dengan ukuran panjang interval referensi atas (2.5.9) untuk suatu proses dalam keadaan terkendali secara statistik (2.2.7), yaitu sebagai:
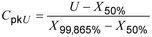
2 : Untuk distribusi normal, rentang referensi atas sama dengan 3S (lihat 2.7.1, Catatan) dan X50 % mewakili rata-rata dan median.
3 : Untuk distribusi non-normal, interval referensi atas dapat diperkirakan menggunakan metode yang dijelaskan dalam ISO/TR 127836) dan X50 % mewakili median.
2.7.5 minimum process capability index (Cpk) : indeks kemampuan proses minimum
lebih kecil dari indeks kapabilitas proses atas (2.7.4) dan indeks kapabilitas proses yang lebih rendah (2.7.3)
2.7.6 process capability ratio : rasio kemampuan proses
kebalikan dari indeks kapabilitas proses (2.7.2)
- Catatan 1 : Rasio kapabilitas proses sering dinyatakan sebagai persentase.
2.7.7 process variation index (Qk) : indeks variasi proses
ukuran variasi (2.2.1) dinyatakan dalam nilai target (3.1.2)
Catatan :
1 : Ketika nilai target, T, tidak sama dengan nol, indeks dinyatakan sebagai:
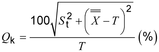
2 : Properti indeks ini adalah ketika proses (2.1.1) menyimpang dari targetnya, atau variasi proses meningkat, nilai indeks akan meningkat. Semakin dekat indeks ke nol, semakin baik kinerja proses relatif terhadap targetnya.
3 : Indeks ini berguna dalam situasi di mana nilai target lebih disukai tetapi tidak ada toleransi yang ditentukan (3.1.6) yang tersedia untuk menilai kemampuan relatif. Situasi seperti itu termasuk dalam pengendalian proses statistik non-produksi (2.1.8) dan tanggapan dari eksperimen yang dirancang.
ISO 3534-2:2006 Klausa 3 – 5
Dikarenakan isi Klausa 1 dan 5 ini terlalu panjang, maka pembaca bisa melanjutkan ke artikel lanjutan dari standarku.com berikut :
- ISO 3534-2 klausa 3
- ISO 3534-2 klausa 4
- ISO 3534-2 klausa 5
Penutup
Demikian artikel dari standarku.com mengenai Standar ISO 3534-2:2006.
Mohon saran dari pembaca untuk kelengkapan isi artikel ini, silahkan saran tersebut dapat disampaikan melalui kolom komentar.
Baca artikel lain :
- International Organization for Standardization
- Memahami apa itu Standar ISO
- Memahami Standard atau Standar
Sumber referensi :