ISO 3534-1:2006 Klausa 2.49 – 2.70 adalah Standar Internasional mengenai kosakata dan simbol statistik, khususnya tentang istilah statistik umum dan istilah yang digunakan dalam probabilitas.
Artikel ini merupakan lanjutan dari artikel sebelumnya berikut :
- ISO 3534-1 istilah probabilitas statistik
- ISO 3534-1:2006 Klausa 1.1 – 1.20
- ISO 3534-1:2006 Klausa 1.21 – 1.40
- ISO 3534-1 Klausa 1.41 – 1.65
- ISO 3534-1 Klausa 2.1-2.9
- ISO 3534-1 Klausa 2.10-2.23
- ISO 3534-1 Klausa 2.24 – 2.48
ISO 3534-1:2006 Klausa 2.49 – 2.70
ISO 3534-1:2006 Klausa 2.49 – 2.50
2.49 negative binomial distribution : distribusi binomial negatif
distribusi diskrit (2.22) memiliki fungsi massa probabilitas (2.24)
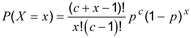
dimana x = 0, 1, 2, …, n dengan parameter c > 0 dan parameter p memenuhi 0 < p < 1.
Catatan :
- 1 : Jika c = 1, distribusi binomial negatif dikenal sebagai distribusi geometrik dan menggambarkan probabilitas (2.5) bahwa kejadian pertama dari peristiwa (2.2) yang probabilitasnya adalah p, akan terjadi dalam percobaan (x + 1 ).
- 2 : Fungsi massa probabilitas juga dapat ditulis dengan cara ekuivalen berikut:
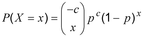
Istilah “distribusi binomial negatif” muncul dari cara penulisan fungsi massa probabilitas ini.
- 3 : Versi fungsi massa probabilitas yang diberikan dalam definisi sering disebut “distribusi Pascal” asalkan c adalah bilangan bulat yang lebih besar dari atau sama dengan 1. Dalam kasus itu, fungsi massa probabilitas menggambarkan probabilitas bahwa cth kejadian dari peristiwa (2.2), yang probabilitasnya (2.5) adalah p, terjadi dalam percobaan (c + x).
- 4 : Rata-rata (2,35) dari distribusi binomial negatif adalah (cp)/(1 p). Varians (2,36) dari binomial negatif adalah (cp)/(1 p)2.
2.50 normal distribution : distribusi normal
Gaussian distribution : Distribusi Gauss
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
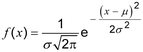
dimana < x < dan dengan parameter < μ < dan > 0.
Catatan :
- 1 : Distribusi normal adalah salah satu distribusi probabilitas yang paling banyak digunakan (2.11) dalam statistik terapan. Karena bentuk fungsi kerapatan, secara informal disebut sebagai kurva “berbentuk lonceng”.
Selain berfungsi sebagai model untuk fenomena acak, ia muncul sebagai distribusi pembatas dari rata-rata (1,15). Sebagai distribusi referensi dalam statistik, ini banyak digunakan untuk menilai keanehan hasil eksperimen.
- 2 : Parameter lokasi adalah mean (2,35) dan parameter skala adalah simpangan baku (2,37) dari distribusi normal.
ISO 3534-1:2006 Klausa 2.51 – 2.52
2.51 standardized normal distribution : distribusi normal standar
standardized Gaussian distribution : distribusi Gaussian standar
distribusi normal (2,50) dengan = 0 dan = 1
- Catatan 1 : Fungsi kepadatan probabilitas (2,26) dari distribusi normal standar adalah
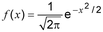
dimana < x < . Tabel distribusi normal melibatkan fungsi kepadatan probabilitas ini, memberikan misalnya, area di bawah f untuk nilai dalam (−∞, ).
2.52 lognormal distribution : distribusi lognormal
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
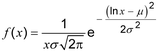
di mana x > 0 dan dengan parameter < < dan > 0.
Catatan :
- 1 : Jika Y memiliki distribusi normal (2,50) dengan mean (2,35) dan simpangan baku (2,37) , maka transformasi yang diberikan oleh X = exp(Y) memiliki fungsi kerapatan probabilitas yang diberikan dalam definisi. Jika X memiliki distribusi lognormal dengan fungsi kerapatan seperti yang diberikan dalam definisi, maka ln(X) memiliki distribusi normal dengan mean dan standar deviasi .
- 2 : Rata-rata dari distribusi lognormal adalah exp[μ + (σ2)/2] dan variansnya adalah exp(2μ + 2) × [exp(σ2) 1]. Hal ini menunjukkan bahwa mean dan varians dari distribusi lognormal merupakan fungsi dari parameter dan 2.
- 3 : Distribusi lognormal dan distribusi Weibull (2.63) umumnya digunakan dalam aplikasi keandalan.
ISO 3534-1:2006 Klausa 2.53 – 2.55
2.53 t distribution : distribusi t
Student’s distribution : Distribusi siswa
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
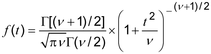
di mana > t > dan dengan parameter , bilangan bulat positif.
Catatan :
- 1 : Distribusi t secara luas digunakan dalam praktik untuk mengevaluasi rata-rata sampel (1,15) dalam kasus umum di mana deviasi standar populasi diperkirakan dari data. Statistik t sampel dapat dibandingkan dengan distribusi t dengan n 1 derajat kebebasan untuk menilai mean tertentu sebagai penggambaran mean populasi yang sebenarnya.
- 2 : Distribusi t muncul sebagai distribusi hasil bagi dua variabel acak independen (2,10), pembilangnya memiliki distribusi normal standar (2,51) dan penyebutnya didistribusikan sebagai akar kuadrat positif dari sebuah chi- distribusi kuadrat (2,57) setelah dibagi dengan derajat kebebasannya. Parameter disebut sebagai derajat kebebasan (2,54).
- 3 : Fungsi gamma didefinisikan dalam 2.56.
2.54 degrees of freedom (ν) : derajat kebebasan
jumlah istilah dalam jumlah dikurangi jumlah kendala pada istilah jumlah
- Catatan 1 : Konsep ini sebelumnya ditemukan dalam konteks penggunaan n 1 dalam penyebut penaksir (1,12) dari varians sampel (1,16). Jumlah derajat kebebasan digunakan untuk memodifikasi parameter. Istilah derajat kebebasan juga banyak digunakan dalam ISO 3534-3 di mana kuadrat rata-rata diberikan sebagai jumlah kuadrat dibagi dengan derajat kebebasan yang sesuai.
2.55 F distribution : distribusi F
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
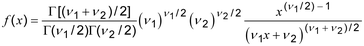
di mana
- x > 0
- 1 dan 2 bilangan bulat positif
- Γ adalah fungsi gamma yang didefinisikan dalam 2.56.
Catatan :
- 1 : Distribusi F adalah distribusi referensi yang berguna untuk menilai rasio varians independen (2,36).
- 2 : Distribusi F muncul sebagai distribusi hasil bagi dua variabel acak independen yang masing-masing memiliki distribusi chi-kuadrat (2,57), dibagi dengan derajat kebebasannya (2,54). Parameter 1 adalah derajat kebebasan pembilang dan 2 adalah derajat kebebasan penyebut dari distribusi F.
ISO 3534-1:2006 Klausa 2.56 – 2.58
2.56 gamma distribution : distribusi gamma
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
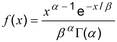
di mana x > 0 dan parameter > 0, > 0.
Catatan :
- 1 : Distribusi gamma digunakan dalam aplikasi keandalan untuk memodelkan waktu hingga kegagalan. Ini mencakup distribusi eksponensial (2,58) sebagai kasus khusus serta kasus lain dengan tingkat kegagalan yang meningkat seiring bertambahnya usia.
- 2 : Fungsi gamma didefinisikan oleh
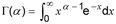
Untuk nilai integer dari , (α) =(α− 1)!
- 3 : Rata-rata (2,35) dari distribusi gamma adalah . Varians (2,36) dari distribusi gamma adalah 2.
2.57 chi-squared distribution : distribusi chi-kuadrat
χ2 distribution
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
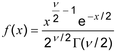
dimana x > 0 dan dengan > 0.
Catatan :
- 1 : Untuk data yang muncul dari distribusi normal (2,50) dengan standar deviasi yang diketahui (2,37)σ, statistik nS2/σ2 memiliki distribusi chi-kuadrat dengan n 1 derajat kebebasan. Hasil ini merupakan dasar untuk memperoleh interval kepercayaan untuk 2. Area aplikasi lain untuk distribusi chi-kuadrat adalah sebagai distribusi referensi untuk uji kecocokan.
- 2 : Distribusi ini merupakan kasus khusus dari distribusi gamma (2,56) dengan parameter = /2 dan = 2. Parameter disebut sebagai derajat kebebasan (2,54).
- 3 : Rerata (2,35) dari distribusi khi-kuadrat adalah . Varians (2,36) dari distribusi chi-kuadrat adalah 2ν.
2.58 exponential distribution distribusi eksponensial
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
f(x) = 1 e x/β
di mana x > 0 dan dengan parameter > 0.
Catatan :
- 1 : Distribusi eksponensial memberikan dasar dalam aplikasi keandalan, sesuai dengan kasus “kurangnya penuaan” atau properti tanpa memori.
- 2 : Distribusi eksponensial adalah kasus khusus dari distribusi gamma (2,56) dengan = 1 atau setara, distribusi chi-kuadrat (2,57) dengan = 2.
- 3 : Rata-rata (2,35) dari distribusi eksponensial adalah . Varians (2,36) dari distribusi eksponensial adalah 2.
ISO 3534-1:2006 Klausa 2.59 – 2.61
2.59 beta distribution : distribusi beta
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
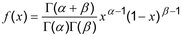
dimana 0 x 1 dan dengan parameter , > 0.
- Catatan 1 : Distribusi beta sangat fleksibel, memiliki fungsi kepadatan probabilitas yang memiliki berbagai bentuk (unimodal, berbentuk “j”, berbentuk “u”). Distribusi dapat digunakan sebagai model dari
ketidakpastian yang terkait dengan proporsi. Misalnya, dalam aplikasi pemodelan badai asuransi, proporsi kerusakan yang diharapkan pada jenis struktur untuk kecepatan angin tertentu mungkin 0,40, meskipun tidak semua rumah yang mengalami medan angin ini akan mengalami kerusakan yang sama. Distribusi beta dengan mean 0,40 dapat digunakan untuk memodelkan disparitas kerusakan pada jenis struktur ini.
2.60 uniform distribution : distribusi seragam
rectangular distribution : distribusi persegi panjang
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
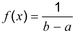
dimana a x b.
Catatan :
- 1 : Distribusi seragam dengan a = 0 dan b = 1 adalah distribusi yang mendasari untuk pembangkit bilangan acak tipikal.
- 2 : Rata-rata (2,35) dari distribusi seragam adalah (a + b)/2. Varians (2,36) dari distribusi seragam adalah (b a)2/12.
- 3 : Distribusi seragam adalah kasus khusus dari distribusi beta dengan = 1 dan = 1.
2.61 type I extreme value distribution : distribusi nilai ekstrim tipe I
Gumbel distribution : Distribusi Gumbel
distribusi kontinu (2.23) memiliki fungsi distribusi (2.7)
F(x) = e e−(x a)/b
dimana > x > dengan parameter > a > , b > 0.
- Catatan 1 : Distribusi nilai ekstrem menyediakan distribusi referensi yang sesuai untuk statistik orde ekstrem (1.9)X(1) dan X(n). Tiga kemungkinan distribusi pembatas karena n cenderung disediakan oleh tiga jenis distribusi nilai ekstrim yang diberikan pada 2.61, 2.62 dan 2.63.
ISO 3534-1:2006 Klausa 2.62 – 2.64
2.62 type II extreme value distribution : distribusi nilai ekstrim tipe II
Fréchet distribution : Distribusi Frechet
distribusi kontinu (2.23) memiliki fungsi distribusi (2.7)
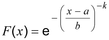
di mana x > a dan dengan parameter > a > , b > 0, k > 0.
2.63 type III extreme value distribution : distribusi nilai ekstrim tipe III
Weibull distribution: Distribusi Weibull
distribusi kontinu (2.23) memiliki fungsi distribusi (2.7)
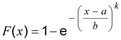
dimana x > a dengan parameter < a < , b > 0, k > 0
Catatan :
- 1 : Selain berfungsi sebagai salah satu dari tiga kemungkinan distribusi pembatas dari statistik orde ekstrim, distribusi Weibull menempati tempat yang menonjol dalam beragam aplikasi, terutama keandalan dan teknik. Distribusi Weibull telah ditunjukkan untuk memberikan kecocokan empiris untuk berbagai set data.
- 2 : Parameter a adalah parameter lokasi dalam artian adalah nilai minimum yang dapat dicapai oleh distribusi Weibull. Parameter b adalah parameter skala [terkait dengan standar deviasi (2,37) dari distribusi Weibull]. Parameter k adalah parameter bentuk.
- 3 : Untuk k = 1, distribusi Weibull terlihat termasuk distribusi eksponensial. Menaikkan distribusi eksponensial dengan a = 0 dan parameter b ke pangkat 1/k menghasilkan distribusi Weibull dalam definisi. Kasus khusus lain dari distribusi Weibull adalah distribusi Rayleigh (untuk a = 0 dan k = 2).
2.64 multivariate normal distribution : distribusi normal multivariat
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
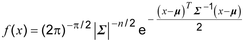
di mana
- −∞ < xi < untuk setiap i;
- μ adalah vektor parameter n-dimensi;
- ∑ adalah n × n simetris, matriks pasti positif dari parameter; dan
- huruf tebal menunjukkan vektor n-dimensi.
Catatan 1 :
- Setiap distribusi marginal (2.18) dari distribusi normal multivariat dalam klausa ini memiliki distribusi normal. Namun, ada banyak distribusi multivariat lain yang memiliki distribusi marginal normal selain versi distribusi yang diberikan dalam klausa ini.
Klausa 2.65 – 2.67
2.65 bivariate normal distribution : distribusi normal bivariat
distribusi kontinu (2.23) memiliki fungsi kepadatan probabilitas (2.26)
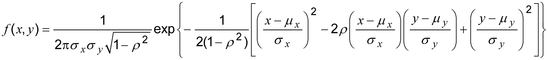
di mana
- −∞ < x < ∞,
- −∞ < y < ∞
- −∞ < μx< ∞,
- −∞ < μy< ∞,
- σx> 0
- σy> 0
- |ρ| < 1
Catatan :
- 1 : Seperti yang ditunjukkan oleh notasi, untuk (X,Y) memiliki fungsi kepadatan probabilitas di atas (2,26), E(X) = x, E(Y) = y, V(X) = x2, V(Y ) = y2, dan adalah koefisien korelasi (2,44) antara X dan Y.
- 2 : Distribusi marginal dari distribusi normal bivariat memiliki distribusi normal. Distribusi bersyarat dari X jika diberikan Y = y terdistribusi normal sebagaimana distribusi bersyarat dari Y jika diberikan X = x.
2.66 standardized bivariate normal distribution : distribusi normal bivariat standar
distribusi normal bivariat (2,65) memiliki komponen distribusi normal standar (2,51)
2.67 sampling distribution : distribusi sampel
distribusi statistik
- Catatan 1 : Ilustrasi distribusi sampling spesifik diberikan dalam Catatan 2 dari 2.53, Catatan 1 dari 2.55 dan Catatan 1 dari 2.57.
Klausa 2.68
2.68 probability space ((Ω, א, ℘)) : ruang probabilitas
ruang sampel (2.1), aljabar sigma terkait peristiwa (2.69), dan ukuran probabilitas (2.70)
Contoh 1:
Sebagai kasus sederhana, ruang sampel dapat terdiri dari semua 105 item yang diproduksi pada hari tertentu di sebuah pabrik.
Aljabar sigma peristiwa terdiri dari semua himpunan bagian yang mungkin. Peristiwa tersebut termasuk {tidak ada item}, {item 1}, {item 2}, … {item 105}, {item 1 dan item 2}, …, {semua 105 item}. Satu kemungkinan ukuran probabilitas dapat didefinisikan sebagai jumlah item dalam suatu peristiwa dibagi dengan jumlah total item yang diproduksi. Misalnya, kejadian {item 4, item 27, item 92} memiliki ukuran probabilitas 3/105.
Contoh 2:
Sebagai contoh kedua, pertimbangkan masa pakai baterai. Jika baterai tiba di tangan pelanggan dan mereka tidak memiliki daya, waktu kelangsungan hidup adalah 0 jam. Jika baterai berfungsi, maka waktu kelangsungan hidup mereka mengikuti
beberapa distribusi probabilitas (2,11), seperti eksponensial (2,58).
Pengumpulan waktu kelangsungan hidup kemudian diatur oleh distribusi yang merupakan campuran antara diskrit (perbandingan baterai yang tidak berfungsi untuk memulai) dan kontinu (waktu kelangsungan hidup yang sebenarnya).
Untuk penyederhanaan dalam contoh ini, diasumsikan bahwa masa pakai baterai relatif pendek dibandingkan dengan waktu studi dan bahwa semua waktu kelangsungan hidup diukur pada kontinum.
Tentu saja, dalam praktiknya kemungkinan waktu kelangsungan hidup yang disensor kanan atau kiri (misalnya, waktu kegagalan diketahui paling sedikit 5 jam atau waktu kegagalan antara 3 dan 3,5 jam) dapat terjadi, dalam hal ini, selanjutnya keuntungan dari struktur ini akan muncul.
Ruang sampel terdiri dari setengah dari garis real (bilangan real lebih besar dari atau sama dengan nol). Aljabar sigma kejadian mencakup semua interval dalam bentuk [0,x) dan himpunan {0}. Selain itu, aljabar sigma mencakup semua gabungan dan perpotongan yang dapat dihitung dari himpunan ini. Ukuran probabilitas melibatkan penentuan untuk setiap set, konstituennya yang mewakili baterai non-fungsional dan baterai yang memiliki waktu kelangsungan hidup positif. Rincian tentang perhitungan yang terkait dengan waktu kegagalan telah diberikan di seluruh klausa ini jika sesuai.
Klausa 2.69
2.69 sigma algebra of events : aljabar sigma kejadian
σ-algebra : -aljabar
sigma field : bidang sigma
σ-field : -bidang
א
set acara (2.2) dengan properti:
- a) milik א;
- b) Jika suatu kejadian milik , maka kejadian komplementernya (2.3) juga milik dari ϐ;
- c) Jika {Ai} adalah sembarang himpunan kejadian di א, maka gabungan
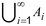
dan irisan
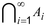
dari kejadian-kejadian tersebut termasuk dalam א.
Contoh :
- 1: Jika ruang sampel adalah himpunan bilangan bulat, maka aljabar sigma peristiwa dapat dipilih sebagai himpunan semua himpunan bagian dari bilangan bulat.
- 2: Jika ruang sampel adalah himpunan bilangan real, maka aljabar sigma kejadian dapat dipilih untuk memasukkan semua himpunan yang bersesuaian dengan interval pada garis real dan semua penyatuan dan perpotongan terhingga dan dapat dihitung dari interval tersebut. Contoh ini dapat diperluas ke dimensi yang lebih tinggi dengan mempertimbangkan “interval” k-dimensi. Secara khusus, dalam dua dimensi, himpunan interval dapat terdiri dari daerah yang didefinisikan oleh {(x,y): x < s, y < t} untuk semua nilai riil s dan t.
Catatan :
- 1 : Aljabar sigma adalah himpunan yang terdiri dari himpunan sebagai anggotanya. Himpunan semua hasil yang mungkin adalah anggota dari aljabar sigma peristiwa, seperti yang ditunjukkan dalam properti a).
- Catatan 2 : Properti c) melibatkan operasi himpunan pada kumpulan himpunan bagian (mungkin terhitung tak terbatas) dari aljabar sigma peristiwa. Notasi yang diberikan menunjukkan bahwa semua persatuan dan perpotongan yang dapat dihitung dari himpunan ini juga termasuk dalam aljabar sigma kejadian.
- Catatan 3 : Properti c) termasuk penutupan (set milik aljabar sigma peristiwa) di bawah baik serikat terbatas atau persimpangan. Sigma kualifikasi digunakan untuk menekankan bahwa A tertutup bahkan di bawah operasi tak terbatas yang dapat dihitung pada himpunan.
Klausa 2.70
2.70 probability measure (℘) : ukuran probabilitas
fungsi non-negatif yang didefinisikan pada aljabar sigma kejadian (2.69) sedemikian rupa sehingga
• a) (Ω) = 1,
di mana Ω menunjukkan ruang sampel (2.1),
•b)
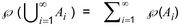
di mana {Ai} adalah urutan kejadian terputus berpasangan (2.2).
Contoh:
- Melanjutkan contoh masa pakai baterai 2.1, pertimbangkan kejadian bahwa baterai bertahan kurang dari satu jam. Peristiwa ini terdiri dari pasangan peristiwa yang terputus {tidak berfungsi} dan {berfungsi kurang dari satu jam tetapi berfungsi pada awalnya}. Secara ekuivalen, peristiwa dapat dilambangkan dengan {0} dan (0,1). Ukuran probabilitas {0} adalah proporsi baterai yang tidak berfungsi pada upaya awal. Ukuran probabilitas dari himpunan (0, 1) tergantung pada distribusi probabilitas kontinu spesifik [misalnya, eksponensial (2,58)] yang mengatur distribusi kegagalan.
Catatan :
- 1 : Ukuran probabilitas memberikan nilai dari [0, 1] untuk setiap peristiwa dalam aljabar sigma peristiwa. Nilai 0 sesuai dengan suatu peristiwa yang tidak mungkin, sedangkan nilai 1 mewakili kepastian terjadinya. Secara khusus, ukuran probabilitas yang terkait dengan himpunan nol adalah nol dan ukuran probabilitas yang ditetapkan untuk ruang sampel adalah 1.
- 2 : Properti b) menunjukkan bahwa jika urutan peristiwa tidak memiliki elemen yang sama ketika dipertimbangkan berpasangan, maka ukuran probabilitas dari gabungan adalah jumlah dari ukuran probabilitas individu. Sebagaimana ditunjukkan lebih lanjut dalam properti b), ini berlaku jika jumlah kejadian tak terhingga.
- 3 : Tiga komponen probabilitas secara efektif dihubungkan melalui variabel acak. Probabilitas (2.5) dari kejadian-kejadian dalam himpunan citra dari variabel acak (2.10) diturunkan dari probabilitas kejadian-kejadian dalam ruang sampel. Suatu kejadian dalam himpunan citra dari variabel acak diberi probabilitas kejadian dalam ruang sampel yang dipetakan ke dalamnya oleh variabel acak.
- 4 : Himpunan gambar dari variabel acak adalah himpunan bilangan real atau himpunan n-tuplet bilangan real terurut. (Perhatikan bahwa set gambar adalah set yang dipetakan oleh variabel acak.)
Penutup
Demikian artikel dari standarku.com mengenai Standar ISO 3534-1:2006.
Mohon saran dari pembaca untuk kelengkapan isi artikel ini, silahkan saran tersebut dapat disampaikan melalui kolom komentar.
Baca artikel lain :
- International Organization for Standardization
- Memahami apa itu Standar ISO
- Memahami Standard atau Standar
Sumber referensi :