Standar deviasi atau simpangan baku adalah suatu rumus dalam ilmu statistika untuk melakukan pengukuran pada kelompok data yang tersebar dari nilai rata-rata.
Pengertian
Istilah Standar Deviasi pertama kali diperkenakan oleh Karl Pearson pada tahun 1894, dalam bukunya : on the dissection of asymmetrical frequency curves.
Dalam bahasa Inggris, standar deviasi disebut standard deviation dan disimbolkan dengan alfabet Yunani sigma σ atau huruf Latin s.
Standar deviasi merupakan sebuah nilai statistik yang di manfaatkan untuk menentukan sebuah sebaran data dalam suatu sampel.
Kemudian juga dapat menentukan seberapa dekat masing-masing titik data tersebut ke rata-rata nilai sampel, nilai rata-rata ini dalam statistik disebut mean.
Sampel adalah data-data yang diambil untuk diukur, jadi tidak semua data diambil namun hanya dicuplik sebagian data saja.
Misalnya ketika kita ingin mengetahui nilai yang didapat siswa di suatu kabupaten dari jumlah seluruh populasi siswa 50.000 orang, maka diambil sampel sebanyak 5.000 orang saja.
Dengan kata lain, Standar deviasi adalah standar yang digunakan untuk mengukur jumlah variasi atau sebaran dari sejumlah nilai data.
Apa hubungan standar deviasi dan variasi?
Semakin rendah nilai standar deviasi maka semakin mendekati rata-rata, sedangkan jika nilai standar deviasi semakin tinggi maka semakin jauh atau lebar rentang variasi datanya.
Oleh karena itu dapat dikatakan bahwa standar deviasi merupakan besarnya perbedaan dari nilai sampel terhadap rata-rata.
Standar deviasi menyatakan keragaman sampel dan dapat digunakan untuk mendapatkan data dari suatu populasi.
Bagaimana cara menghitungnya?
Cara menghitung standar deviasi adalah degan dihitung sebagai akar kuadrat dari varian dengan menentukan variasi antara setiap titik data relatif terhadap rata-rata.
Jika titik data lebih jauh dari rata-rata, ada penyimpangan yang lebih tinggi dalam kumpulan data.
Dengan demikian, semakin menyebar data maka semakin tinggi pula nilai standar deviasi nya.
Ilmu Statistika
Didalam ilmu statistika dan probabilitas, simpangan baku atau deviasi standar adalah ukuran sebaran statistik yang paling umum yang digunakan untuk mengukur bagaimana nilai-nilai data tersebar.
Bisa juga didefinisikan sebagai rata-rata jarak penyimpangan titik-titik data yang diukur dari nilai rata-rata data tersebut.
Dari sudut pandang rumus statistik, deviasi standar didefinisikan sebagai akar kuadrat varians.
Seperti halnya varians, standar deviasi juga merupakan suatu ukuran dispersi atau variasi.
Standar deviasi merupakan ukuran dispersi yang paling banyak dipakai, karena standar deviasi mempunyai satuan ukuran yang sama dengan satuan ukuran data asalnya.
Standar deviasi merupakan bilangan tak-negatif dan memiliki satuan yang sama dengan data, jadi misalnya suatu data diukur dalam satuan meter maka simpangan baku juga diukur dalam meter.
Sebaliknya varians memiliki satuan kuadrat dari data asalnya, misalnya untuk satuan data meter (m) maka varians mengunakan satuan m2.
Simbol standar deviasi untuk populasi adalah σ dan untuk sampel adalah s.
Standar deviasi adalah ukuran penyebaran data yang paling banyak digunakan di statistik, semua gugus data dipertimbangkan sehingga lebih stabil dibandingkan dengan ukuran lainnya.
Namun, apabila dalam gugus data tersebut terdapat nilai ekstrem, standar deviasi menjadi tidak sensitif lagi seperti halnya pada nilai mean (rata-rata).
Standar deviasi adalah nilai statistika yang digunakan untuk menentukan bagaimana persebaran data dalam suatu sampel.
Kemudian melihat seberapa dekat data-data tersebut dengan mean atau rata-rata dari sampel tersebut.
Sederhananya, rumus yang biasa disebut dengan simpangan baku ini berfungsi untuk menentukan seberapa heterogen elemen data yang ada dalam sebuah data.
Menghitung standar deviasi
Cara menghitung standar deviasi dapat dilakukan dengan mudah sebagaimana berikut :
- Pertama adalah menghitung nilai rata-rata dari semua titik data.
- Rata-rata sama dengan jumlah dari semua nilai dalam kumpulan data lalu dibagi dengan jumlah total titik data tersebut.
- Langkah berikutnya adalah menghitung penyimpangan setiap titik data dari rata-rata, caranya adalah dengan mengurangkan nilai dari nilai rata-rata.
- Deviasi setiap titik data akan dikuadratkan dan dicari penyimpangan kuadrat individu rata-rata, lalu nilai yang dihasilkan disebut sebagai varians.
- Sedangkan standar deviasi dapat dihitung dengan akar kuadrat dari varians.
Hubungan Standar Deviasi dan Varian antara lain adalah :
- Varian diturunkan dengan mengambil rata-rata dari titik-titik data, mengurangi rata-rata dari setiap titik data masing-masing, hiung kuadrat masing-masing hasil dan kemudian ambil rata-rata lain dari data-data tersebut. Sedangkan Standar deviasi adalah akar kuadrat dari varian.
- Varian membantu menentukan ukuran penyebaran data bila dibandingkan dengan nilai rata-rata. Ketika varians semakin besar, semakin banyak variasi dalam nilai data terjadi, dan mungkin ada kesenjangan yang lebih besar antara satu nilai data dan lainnya. Jika nilai data semuanya berdekatan, varians akan lebih kecil. Namun, ini lebih sulit untuk dipahami daripada standar deviasi, karena varian mewakili hasil kuadrat yang mungkin tidak dinyatakan secara jelas pada grafik yang sama dengan kumpulan data aslinya. Standar deviasi biasanya lebih mudah untuk digambarkan dan diterapkan.
- Standar deviasi dinyatakan dalam satuan pengukuran yang sama dengan data, yang belum tentu sama dengan variansnya.
- Menggunakan standar deviasi, ahli statistik dapat menentukan apakah data memiliki kurva normal atau hubungan matematika lainnya.
- Jika data berperilaku dalam kurva normal, maka 68% dari titik data akan jatuh dalam satu standar deviasi dari rata-rata, atau titik data rata-rata.
- Varians yang lebih besar menyebabkan lebih banyak titik data berada di luar standar deviasi, sedangkan Varians yang lebih kecil menghasilkan lebih banyak data yang mendekati rata-rata.
Fungsi Standar Deviasi
Ada banyak kegunaan standar deviasi, berikut adalah berbagai manfaat nya dalam beberapa bidang seperti :
Statistik
Dalam ilmu statistik dapat digunakan untuk memberikan gambaran tentang :
- Persebaran data terhadap data rata-rata.
- Kualitas data sampel yang diperolehnya.
- Nilai ketidakpastian pada saat melakukan pengukuran berulang.
Penelitian
Rumus ini bisa mempermudah seseorang ketika melakukan sebuah penelitian, dengan rumus ini maka dapat dicari rata-rata jarak penyimpangan pada data yang telah didapatkan.
Dunia Investasi
Selain digunakan pada analisis statistik, standar deviasi juga dapat digunakan untuk menentukan jumlah risiko dan volatilitas terkait dengan investasi tertentu.
Investor dapat menghitung standar deviasi tahunan pengembalian investasi dan menggunakan angka itu untuk menentukan seberapa stabil investasi tersebut.
Angka standar deviasi yang lebih besar akan berarti investasi yang lebih berisiko, dengan asumsi stabilitas itu adalah hasil yang diinginkan.
Cuaca
Contoh dalam menentukan suhu tinggi harian rata-rata untuk dua kota, satu daratan dan satu di dekat laut.
Standar deviasi dapat membantu untuk memahami bahwa kisaran suhu tinggi harian untuk kota-kota di dekat laut lebih kecil daripada untuk kota-kota di pedalaman.
Kedua kota ini masing-masing dapat memiliki suhu tinggi harian rata-rata yang sama, namun standar deviasi suhu tinggi harian untuk kota pantai akan lebih kecil daripada kota pedalaman.
Dunia balap motor
Dalam balap motor, dilakukan pengukuran terhadap waktu yang dibutuhkan pengemudi untuk menyelesaikan setiap putaran didalam trek.
Pengemudi dengan standar deviasi rendah maka waktu putaran akan lebih konsisten daripada pengemudi dengan standar deviasi yang lebih tinggi.
Informasi yang diperoleh dapat digunakan untuk membantu memahami bagaimana cara pengemudi dapat mengurangi waktu untuk menyelesaikan putaran.
Manajemen Keuangan
Dalam Keuangan, standar deviasi dapat berarti risiko bahwa harga akan naik atau turun seperti contoh mengenai : saham, obligasi, properti, dan lainnya.
Hal ini juga dapat berarti ada risiko bahwa sekelompok harga akan naik atau turun (reksa dana yang dikelola secara aktif, reksa dana indeks, atau ETF).
Risiko adalah salah satu alasan bagi seseorang untuk membuat keputusan tentang apa yang akan dibeli.
Risiko merupakan angka yang dapat digunakan orang untuk mengetahui berapa banyak uang yang mereka dapatkan atau justru berapa banyak uang yang hilang.
Ketika risiko semakin besar, akan didapatkan laba atas investasi yang lebih pula (standar deviasi “plus”).
Namun isa jadi akan mengalami kehilangan lebih banyak uang dari yang diharapkan (standar deviasi “minus”).
Metode Menghitung Standar Deviasi
Ada berbagai macam metode yang dapat digunakan untuk menghitung Standar Deviasi yaitu :
Rumus Standar Deviasi (Simpangan Baku)
Dalam pembentukan rumus standar deviasi ini didasarkan pada rumus variansi, karena standar deviasi adalah akar kuadrat dari variansi.
Untuk mengetahui cara menghitungnya maka ada dua rumus yang harus diketahui, yakni rumus varian dan rumus standar deviasi.
Rumus :

Keterangan Rumus diatas :
- s2 = Varian
- s = Standar deviasi
- S = standar deviasi untuk sampel
- σ = standar deviasi untuk populasi
- fi = Frekuensi
- xi = Nilai x ke – i
- x¯ = Rata-rata (mean) sampel
- μ = rata-rata populasi
- n = Jumlah data
Contoh
Cara Menghitung Standar Deviasi dari data berikut : 4.4 , 5.3 , 5.2 , 4.8.
Cari nilai rata-ratanya : X̄ = ΣX : n = 4.4+5.3+5.2+4.8 : 4 = 4.925
Gunakan rumus standar deviasi tunggal :

Gunakan rumus standar deviasi Populasi :
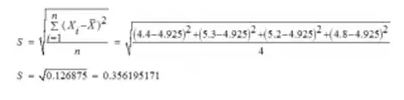
Menghitung Standar Deviasi dengan Kalkulator
Salah satu cara menghitung standar deviasi adalah dengan bantuan alat hitung elektronik yaitu kalkulator.
Kalkulator yang bisa digunakan adalah kalkulator sains (scientific calculator).
Atau kalian bisa download aplikasi kalkulator scientific atau juga memanfaatkan kalkulator scientific online.
Berikut cara menghitung standar deviasi menggunakan alat bantu kalkulator:
- Langkah pertama, nyalakan kalkulator dan klik tombol Mode yang ada di ujung kanan atas.
- Pilih mode statistik dengan menekan tombol nomor 3 (STAT).
- Tekan tombol nomor 1 (VAR-1).
- Masukkan data yang ingin dihitung dengan cara memasukkan angka
- Tekan tombol sama dengan ( = ), masukkan angka lagi, dan begitu seterusnya. Jangan lupa untuk menekan tombol sama dengan ( = ) jika data yang ingin di hitung telah di masukkan.
- Tekan tombol AC, kemudian tombol SHIFT.
- Untuk mengetahui hasil akhir, tekan tombol 1 (STAT), 4 (VAR), (σ x).
- Terakhir tekan tombol sama dengan ( = ).
Cara Menghitung Standar Deviasi Mengunakan Excel
Untuk menggunakan software microsoft excel dibutuhkan komputer atau laptop yang sudah terinstal software aplikasi tersebut.
Rumus atau formula untuk menghitung standar deviasi di Excel adalah STDEV, ketik :
= STDEV (number1, number2,…)
Number1, number2, … adalah 1-255 argumen yang sesuai dengan sampel populasi.
Dapat juga menggunakan array tunggal atau referensi ke array, bukan argumen yang dipisahkan oleh koma.
Keterangan :
- STDEV mengasumsikan bahwa argumen adalah contoh dari populasi. Jika data anda mewakili seluruh populasi, untuk menghitung deviasi standar menggunakan STDEVP.
- Standar deviasi dihitung menggunakan metode “n-1” .
- Argumen dapat berupa nomor atau nama, array, atau referensi yang mengandung angka.
- Nilai-nilai logis dan representasi teks dari nomor yang Anda ketik langsung ke daftar argumen akan dihitung.
- Jika argumen adalah sebuah array atau referensi, hanya nomor/angka dalam array atau referensi yang akan dihitung.
- Sel kosong, nilai-nilai logis, teks, atau nilai-nilai kesalahan dalam array atau referensi akan diabaikan.
- Argumen yang kesalahan nilai atau teks yang tidak dapat diterjemahkan ke dalam nomor/angka akan menyebabkan kesalahan.
- Jika ingin memasukkan nilai-nilai logis dan representasi teks angka dalam referensi sebagai bagian dari perhitungan, gunakan fungsi STDEVA.
Langkah-langkah dalam menghitungnya adalah degan melihat contoh sebagai berikut :
Berdasarkan pengambilan sampel nilai ujian mata pelajaran beberapa siswa di sekolah diketahui data sebagai berikut : 80, 60, 80, 90, 70, 80, 95.
Pertama buka aplikasi dan masukkan data ke dalam tabel excel.
Contohnya seperti tabel di bawah :
| DATA | |
| A | 80 |
| B | 60 |
| C | 80 |
| D | 90 |
| E | 70 |
| F | 80 |
| G | 95 |
| STDEV | 11,7 |
Caranya dengan menekan tombol = STDEV( number1; number 2; dst ).
Maka secara otomatis akan keluar hasil dari contoh diatas, yaitu : 11,70.
( number1; number 2; dst ) adalah excel cell dari data sampel yang kita masukkan.
Penutup
Demikian artikel dari standarku.com mengenai mengenal dasar-dasar ilmu statistik Standar deviasi.
Mohon saran dari pembaca untuk kelengkapan isi artikel ini, silahkan saran tersebut dapat disampaikan melalui kolom komentar.
Baca artikel lain :
Sumber referensi :
Maaf, Anda mengatakan dalam tulisan Anda bahwa “Dalam bahasa Inggris, standar deviasi disebut deviation standard”. Pernyataan Anda ini jelas tidak didukung oleh sumber ilmu manapun. TIDAK ADA ISTILAH “DEVIATION STANDARD” baik itu dalam Statistika maupun dalam Bahasa Inggris. Yang ada adalah STANDARD DEVIATION yang jika diterjemahkan ke dalama bahasa Indonesia menjadi Deviasi Standar atau Deviasi Baku atau Simpangan Baku. Terjemahan yang Anda gunakan itu, yakni “standar deviasi” secara tatabahasa Indonesia SALAH. Silakan Anda berdiskusi dengan mereka yang memahami Bahasa Inggris, Bahasa Indonesia dan juga Statisitika tentang istilah tersebut. Terima kasih.-
baik, terimakasih atas masukannya, akan kami review kembali isi artikel tersebut