Statistika Dasar untuk Six Sigma digunakan sebagai persiapan belajar dasar-dasar istilah dalam six sigma yang berkaitan erat dengan Statistika.
Artikel ini melengkapi dan menmpermudah untuk memahami isi artikel lain dari standarku.com berikut :
Mengapa Menggunakan Statistika Dasar?
Tujuan penggunaan Statistika adalah untuk memprediksi dan mencegah, jadi bukan sekedar melakukan inspeksi dan deteksi.
Statistika adalah ilmu yg membahas tentang pengumpulan, penyusunan, analisa, interpretasi dan penyajian data.
Terdapat 2 klasifikasi yakni :
- Statistika Descriptive : memberikan informasi tentang kinerja dari sebuah proses
- Statistika Inferensial : memberikan informasi tentang prediksi tentang kinerja sebuah proses (Peluang).
Data
Pengumpulan Data dalam Statistika Dasar
Mengapa Perlu Mengumpulkan Data ? tujuan dari pengumpulan data adalah untuk :
- mengumpulkan fakta-fakta tentang suatu masalah atau kesempatan yang dapat dikuantifikasi
- menyampaikan fakta-fakta ini dalam bahasa yang sama
- menetapkan informasi mendasar tentang sebuah proses
- mengukur jumlah dan arah perubahan-perubahan yang terjadi
- membandingkan gambaran proses sebelumnya dan sesudahnya
- memfasilitasi analisa keuntungan (Cost Benefit Analysis) dari solusi yang diusulkan
- mengkuantifikasi dampak dari sebuah solusi
selanjutnya, ditentukan :
- Apakah data-data dalam proses yang ada sekarang sudah tersedia ?
- Apakah data-data yang ada sekarang sudah cukup menggambarkan proses yang bersangkutan ?
- Sudahkah kita menetapkan kategori data apa yang diperlukan untuk dikumpulkan ?
Contoh :
- Defects
- Waktu
- Biaya (Cost)
- Efisiensi
- Kinerja (Performance)
Perhatikan bahwa data hanya dikumpulkan jika kita akan menggunakannya saja.
Jenis Data
Berdasarkan jenisnya, data dapat dibagi menjadi :
- Data Kualitatif (Atribut), yaitu data yang berbentuk kategori atau kualitas (tidak berbentuk bilangan). contoh : Bagus, Manis, Pahit, Cantik, Tinggi, Setuju, dan lainnya.
- Data Kuantitatif (Variabel), yaitu data yang berbentuk bilangan (angka) baik hasil penghitungan maupun hasil pengukuran. Contoh : 200 anak, 350 kg, 23 derajat, 20 CTV, dan lainnya.
Berdasarkan cara memperoleh datanya, data kuantitatif (Variabel) dapat dibagi menjadi :
- Data Diskrit (Discrete Data), yaitu data yang diperoleh berdasarkan hasil penghitungan atau penjumlahan terhadap objek yang dipelajari. Contoh : 200 orang, 369 CTV, 500 mobil, dan lainnya. Jadi yang ditanyakan adalah ‘Berapa Banyak ?’
- Data Kontinyu (Continous Data), yaitu data yang diperoleh berdasarakan hasil pengukuran terhadap objek yang dipelajari. Contoh : 250 milimeter, 35 derajat celcius, 20 DB, 58 kg, dan lainnya. Jadi yang ditanyakan adalah ‘Berapa Ukurannya ?’.
Kesimpulan Data
Berdasarkan ukuran letak, terdapat : Mean, Median, Modus.
Sedangkan berdasarkan ukuran Penyebaran, terdapat : Range, Variance, Standard Deviation.
Mean, Median, Modus dalam Statistika Dasar
Rata-rata (Mean)
Mean adalah jumlah semua data dibagi banyaknya data, hasilnya sangat dipengaruhi oleh nilai-nilai yang ekstrim.
Formula perhitungannya adalah :
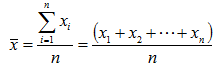
Median
Median adalah nilai tengah dari sederetan data yang sudah terurut dari nilai terkecil hingga terbesar (diranking), yang tidak dipengaruhi oleh nilai-nilai yang ekstrim.
Ketentuan dalam Median :
- Jika banyaknya data adalah ganjil, median sama dengan nilai data yang berada di tengah-tengah
- Jika banyaknya data adalah genap, median sama dengan rata-rata 2 nilai yang berada paling tengah
Formula perhitungannya adalah :
- Pada jumlah data yang ganjil, maka Median adalah Nilai Tengah.
- Sedangkan, pada jumlah data yang genap, maka Median adalah jumlah 2 nilai yang ada di posisi paling tengah kemudian dibagi 2.
Modus (Mode)
Modus merupakan Nilai yang paling banyak atau yang paling sering muncul.
Rentang (Range)
Range adalah “Nilai Terbesar” dikurangi “Nilai Terkecil”.
Varians (Variance)
Variance adalah Rata-rata kuadrat dari deviasi setiap nilai dari nilai rata-ratanya.
Formula perhitungannya adalah :
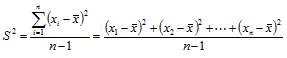
Simpangan Baku (Standard Deviation)
Standard Deviation adalah Akar kuadrat dari varians, yakni rata-rata jarak data dari nilai rata-ratanya.
Formula perhitungannya adalah :
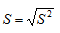
Lebih jelas mengenai Standard Deviation dapat dibaca pada artikel lain dari standarku.com berikut :
Jenis-jenis Distribusi dalam Statistika Dasar
Disini digunakan Histogram, yang bisa bermanfaat untuk menjelaskan distribusi data.
Berikut contoh beberapa bentuk Distribusi :
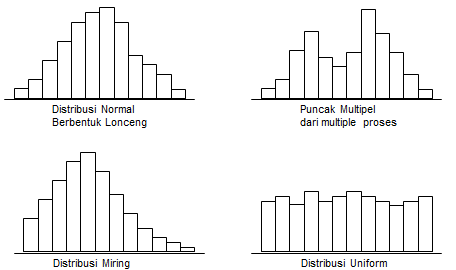
Banyak kejadian yang muncul secara acak (Random) menghasilkan data dengan distribusi sebagai berikut :
- Bell shaped
- Symmetrical
Kurva yang menghubungkan puncak-puncak batang disebut Kurva Peluang Normal yang digunakan untuk meng-estimasi Distribusi Normal dari kejadian-kejadian yang muncul secara acak (Random)
- Distribusinya simetris terhadap rata-ratanya
- Ujung kurvanya asymptotic terhadap sumbu-X
- Mean = Median = Mode
- Peluang dibawah kurva = 1
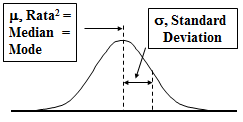
Distribusi Normal
Kita dapat menggunakan rata-rata sampel dan standar deviasi untuk menjelaskan populasinya dan menggambarkan histogramnya (data diskrit) untuk melihat distribusi normalnya (data kontinyu).
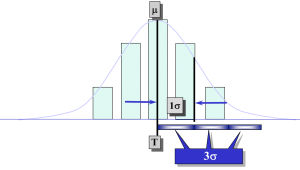
Sifat-sifat Distribusi Normal :
- 68.26 % data akan berada diantara +1s dan -1s dari rata-ratanya
- 95.44 % data akan berada diantara +2s dan -2s dari rata-ratanya
- 99.73 % data akan berada diantara +3s dan -3s dari rata-ratanya
- 99.9937 % data akan berada diantara +4s dan -4s dari rata-ratanya
- 99.999943 % data akan berada diantara +5s dan -5s dari rata-ratanya
- 99.9999998 % data akan berada diantara +6s dan -6s dari rata-ratanya
Letak dan Penyebaran Proses dalam Statistika Dasar
Berikut gambaran pemahaman keduanya :
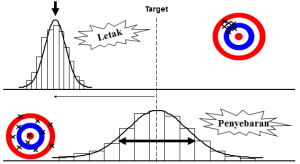
Penjelasan :
- gambar atas menunjukkan bahwa data yang dihasilkan variasinya kecil namun tidak sesuai target atau tidak tepat sasaran.
- sedangkan pada gambar bawah menunjukkan bahwa data yang dihasilkan sesuai target atau tepat sasaran, namun variasinya besar atau lebar.
Populasi & Sampel
Populasi adalah semua unit yang berada dalam sebuah kelompok yang sedang kita perhatikan atau pelajari.
Sampel adalah sebagian unit yang dipilih dari sebuah populasi.
Contoh :
- Populasi : Semua part yang dikirim oleh suplier pada suatu pengiriman
- Sampel : 100 Back Cover yang dipilih dari sebuah pengiriman.
Beberapa alasan mengapa kita mempelajari Sampel :
- Mempelajari populasi akan memakan biaya terlalu tinggi
- Keakuratan prediksi berdasarkan sampel biasanya sama dengan informasi yang diperoleh berdasarkan seluruh populasi
Simbol-simbol yang digunakan :
- Rata-rata dan Simpangan Baku populasi dilambangkan dengan m & s
- Rata-rata dan Simpangan Baku sampel dilambangkan dengan & s
Kesimpulan Statistika Dasar (Statistical Inference) :
- Inference : dilakukan untuk memahami sifat-sifat sebuah populasi melalui sifat-sifat sebuah sampel yang dipilih dari populasi tersebut.
- Nilai Inferensial : Statistik, yaitu sebuah nilai yang diperoleh dari sebuah sampel.
- Target inferensial : Parameter, yaitu sebuah nilai yang diperoleh dari sebuah populasi (m , s, …, dll)
- Uji Hipotesis : Untuk membuktikan kebenaran dari pernyataan seseorang tentang sesuatu hal
- Yang diperlukan dalam sebuah inferensial : Data dan Distribusi Peluang.
- Peluang (p) : Perbandingan jumlah sebuah kejadian diantara semua kejadian yang mungkin terjadi, Nilainya = 0 £ p £ 1, Contoh : pada saat seseorang melemparkan sebuah koin, berapa peluang bahwa sisi angka akan berada di bagian atas.
Lebih jelas mengenai Hipotesis dapat dibaca pada artikel lain dari standarku.com berikut :
Penutup
Demikian artikel dari standarku.com mengenai Statistika Dasar untuk Six Sigma.
Mohon saran dari pembaca untuk kelengkapan isi artikel ini, silahkan saran tersebut dapat disampaikan melalui kolom komentar.
Baca artikel lain :
- DMAIC Six Sigma
- ISO 13053-1 DMAIC Six Sigma
- ISO 13053-2 alat dan teknik Six Sigma
- ISO 10017 panduan teknik statistik
- Memahami Standard atau Standar
Sumber referensi :